Tag: computer science
Josh Alman Awarded The 2024 Packard Fellowship
Microsoft Says It’s Cracked The Code On An Important Quantum Computing Problem
Microsoft and Quantinuum say they’ve figured out how to make qubits that are less prone to error.
Game Theory, Blockchain Expert Tim Roughgarden Elected as ACM Fellow
The ACM recognizes fellows for their transformative contributions to computing science and technology.
Mihalis Fest 2023
The three-day celebration honors the contributions of Mihalis Yannakakis to science on the occasion of his 70th birthday.
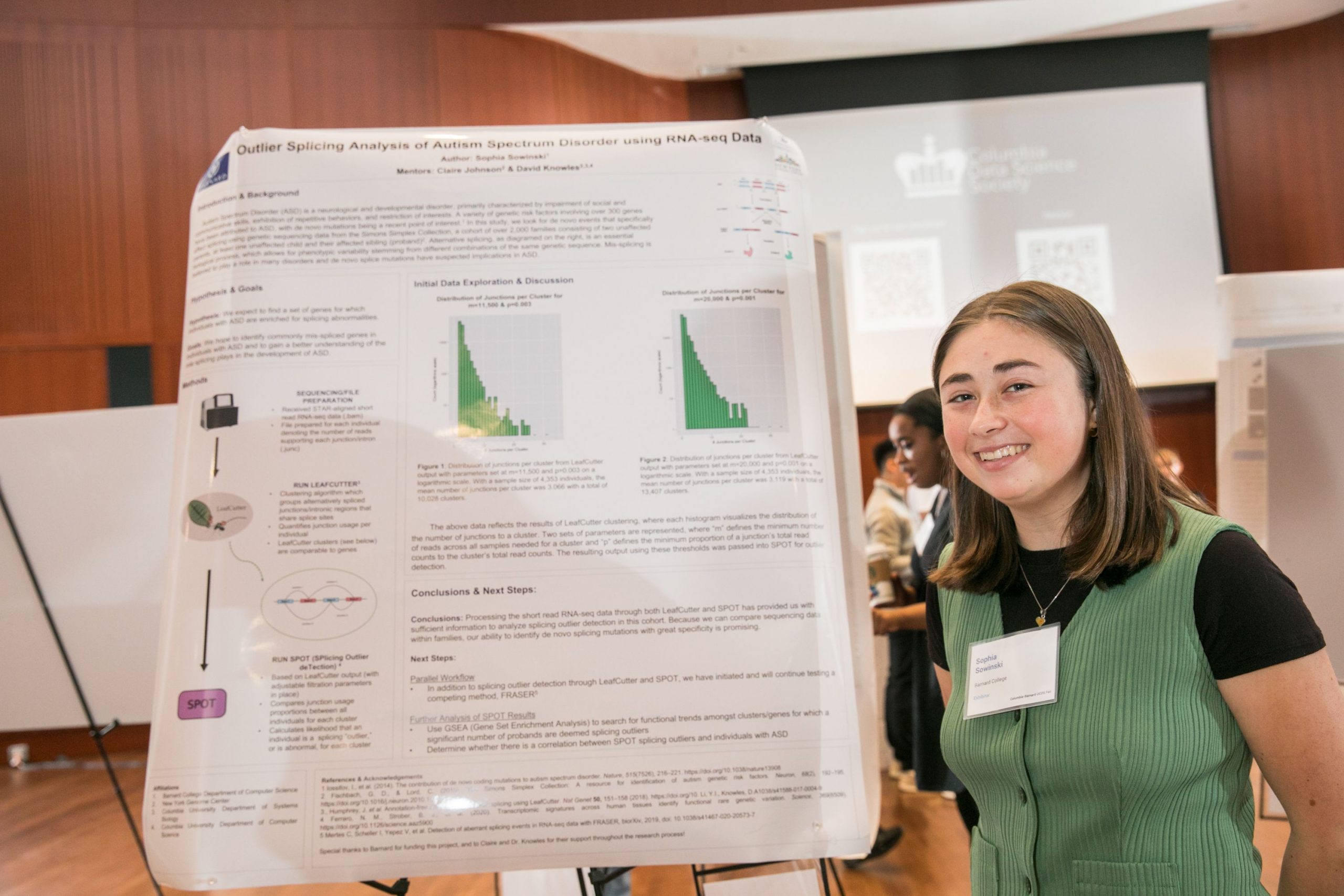
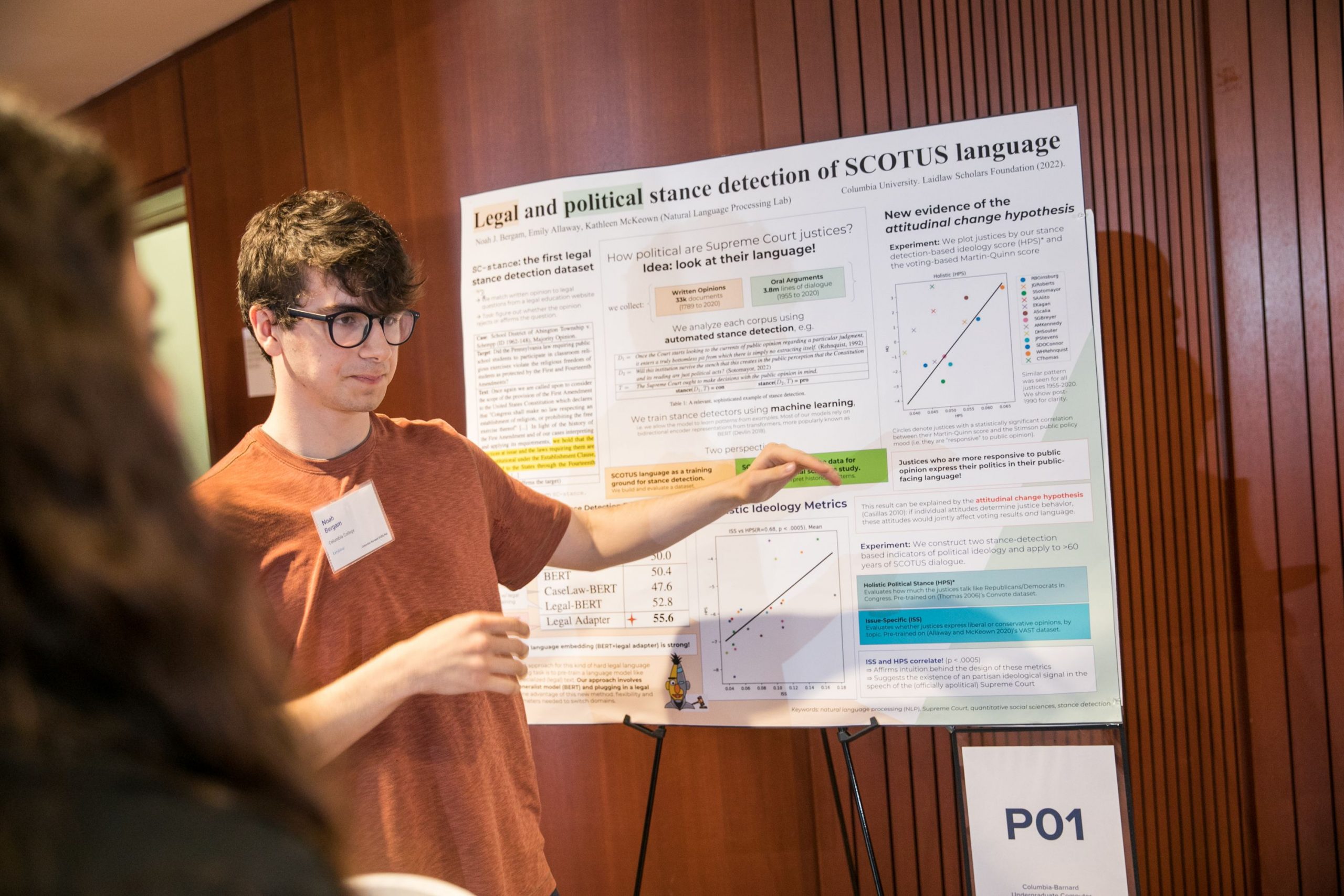
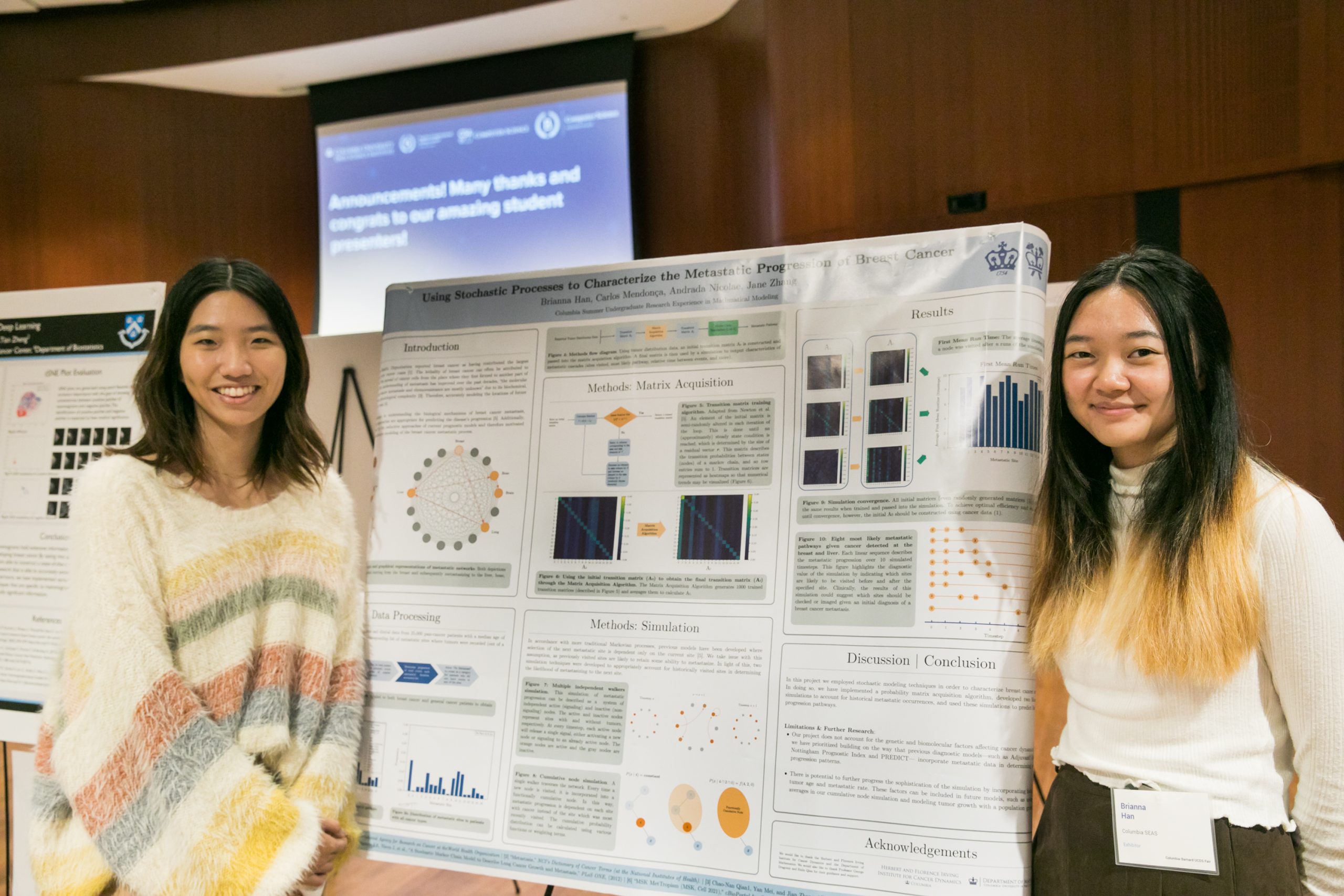
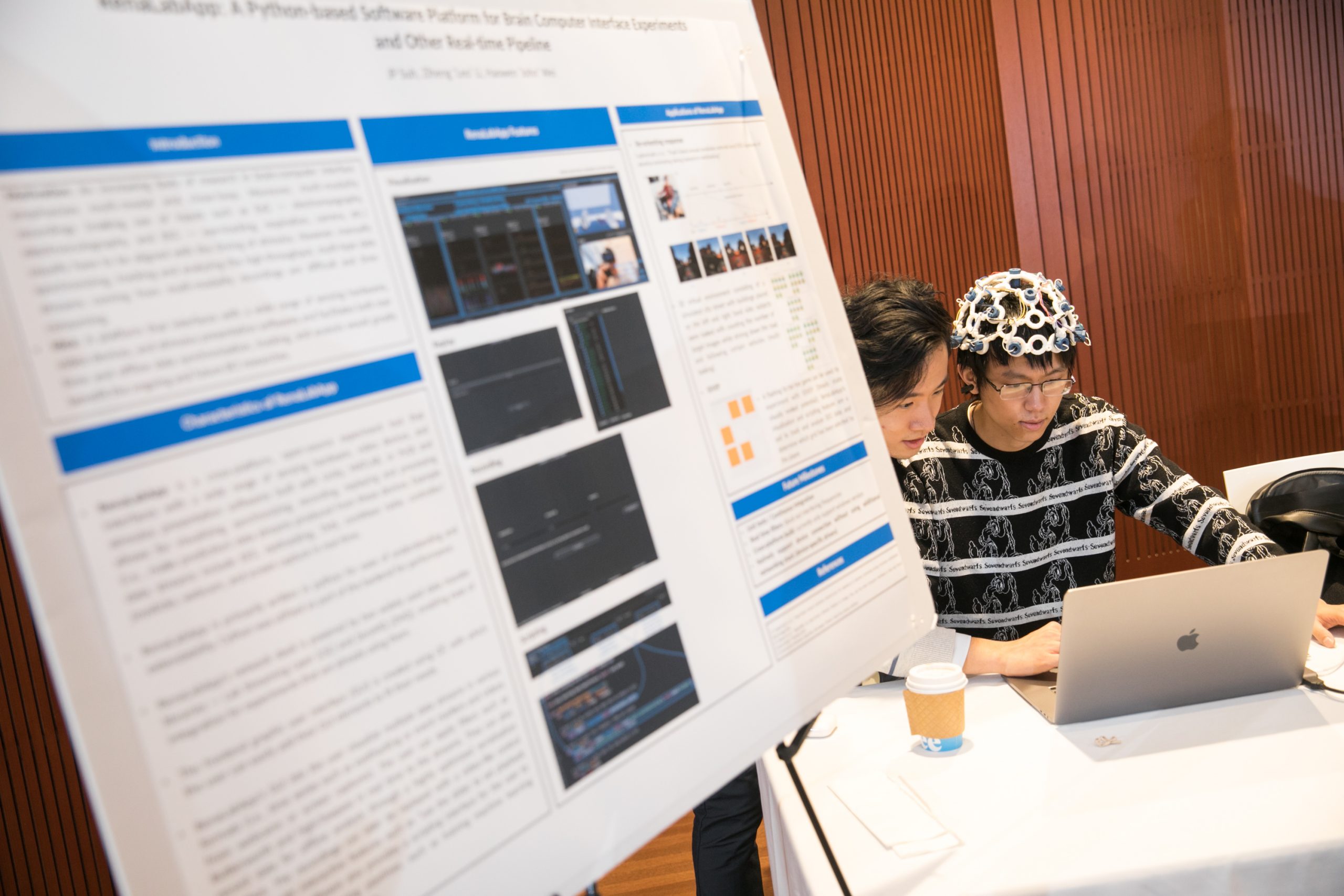
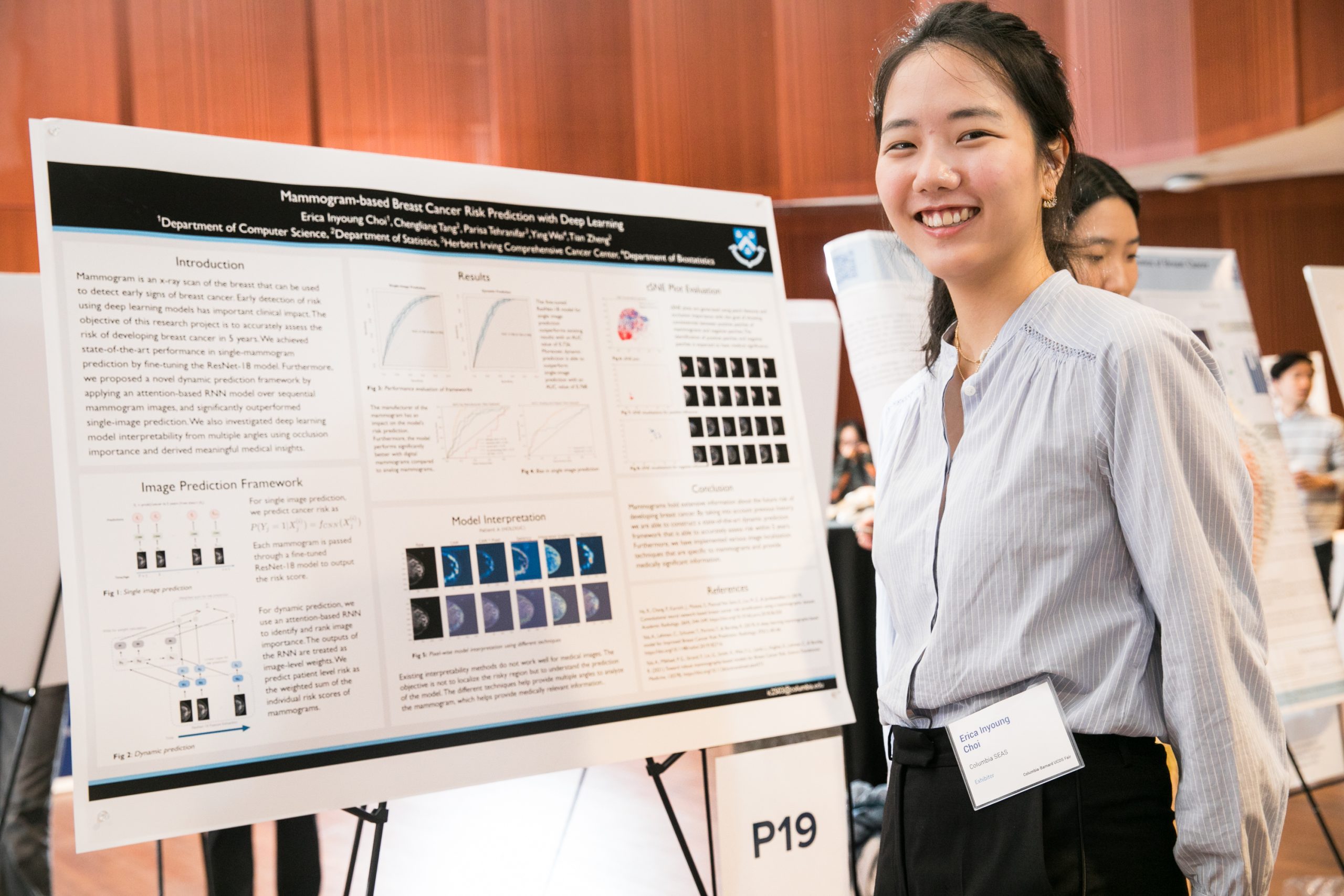
The Undergraduate Computer and Data Science Research Fair
The inaugural fair gave students the opportunity to take their research from paper to presentation and showcase their hard work.
The projects of the Undergraduate Computer and Data Science Research Fair fell under the themes of Data Science and Society, Interdisciplinary Data Science Applications, Data Science and Computer Science Research. Posters and demonstrations were proudly hosted by twenty-five students from SEAS, Barnard College, Columbia College, and the School of General Studies.




The fair was organized by the Data, Media and Society Center at the Data Science Institute, Columbia University; the Barnard Program in Computer Science and the Vagelos Computational Science Center; and the Department of Computer Science at Columbia Engineering led by Eugene Wu, Susan McGregor, Rebecca Wright, and Alexis Avedisian.
CS Researchers Receive Test of Time Awards
Five CS researchers received Test of Time awards for papers that have had a lasting impact on their fields. The influential papers were presented at their respective conferences in the past 25 years and have remained relevant to research and practice.

IACR International Conference on Practice and Theory of Public-Key Cryptography (PKC2020)
Test of Time award
Yiannis Tsiounis & Moti Yung

41st IEEE Symposium on Security and Privacy
(IEEE S&P 2020)
Test of Time award
Adam Young & Moti Yung

16th ACM conference on Computer and Communications Security (ACM CCS 2019)
Test of Time award
Thomas Ristenpart, Eran Tromer, Hovav Shacham, Stefan Savage

International Conference on Computer Vision
(ICCV 2019)
Helmholtz Prize
Neeraj Kumar, Alexander C. Berg, Peter N. Belhumeur, Shree K. Nayar

IEEE International Symposium on Mixed and Augmented Reality (IEEE ISMAR 2019)
Lasting Impact Paper Award
Steven J. Henderson & Steven Feiner
Are you looking for a thrilling and unforgettable experience? Look no further than fire scatters casino at https://fire-scatters.com. Our games are sure to excite and engage you like never before.
Papers from the Theory of Computing Group Accepted to SODA 2020
Nine papers from CS researchers were accepted to the ACM-SIAM Symposium on Discrete Algorithms (SODA20), held in Salt Lake City, Utah. The conference focuses on algorithm design and discrete mathematics.
Learning From Satisfying Assignments Under Continuous Distributions
Clement Canonne Stanford University, Anindya De University of Pennsylvania, Rocco A. Servedio Columbia University
A common type of problem studied in machine learning is learning an unknown classification rule from labeled data. In this problem paradigm, the learner receives a collection of data points, some of which are labeled “positive” and some of which are labeled “negative”, and the goal is to come up with a rule which will have high accuracy in classifying future data points as either “positive” or “negative”.
In a SODA 2015 paper, De, Diakonikolas, and Servedio studied the possibilities and limitations of efficient machine learning algorithms when the learner is only given access to one type of data point, namely points that are labeled “positive”. (These are also known as “satisfying assignments” of the unknown classification rule.) They showed that certain types of classification rules can be learned efficiently in this setting while others cannot. However, all of the settings considered in that earlier work were ones in which the data points themselves were defined in terms of “categorical” features also known as binary yes-no features (such as “hairy/hairless” “mammal/non-mammal” “aquatic/non-aquatic” and so on).
In many natural settings, though, data points are defined in terms of continuous numerical features (such as “eight inches tall” “weighs seventeen pounds” “six years old” and so on).
This paper extended the earlier SODA 2015 paper’s results to handle classification rules defined in terms of continuous features as well. It shows that certain types of classification rules over continuous data are efficiently learnable from positive examples only while others are not.
“Most learning algorithms in the literature crucially use both positive and negative examples,” said Rocco Servedio. “So at first I thought that it is somewhat surprising that learning is possible at all in this kind of setting where you only have positive examples as opposed to both positive and negative examples.”
But learning from positive examples only is actually pretty similar to what humans do when they learn — teachers rarely show students approaches that fail to solve a problem, rarely have them carry out experiments that don’t work, etc. Continued Servedio, “So maybe we should have expected this type of learning to be possible all along.”
Nearly Optimal Edge Estimation with Independent Set Queries
Xi Chen Columbia University, Amit Levi University of Waterloo, Erik Waingarten Columbia University
The researchers were interested in algorithms which are given access to a large undirected graph G on n vertices and estimate the number of edges of the graph up to a small multiplicative error. In other words, for a very small ϵ > 0 (think of this as 0.01) and a graph with m edges, they wanted to output a number m’ satisfying (1-ε) m ≤ m’ ≤ (1+ε) m with probability at least 2/3, and the goal is to perform this task without having to read the whole graph.
For a simple example, suppose that the access to a graph allowed to check whether two vertices are connected by an edge. Then, an algorithm for counting the number of edges exactly would need to ask whether all pairs of vertices are connected, resulting in an (n choose 2)-query algorithm since these are all possible pairs of vertices. However, sampling Θ((n choose 2) / (m ε2)) random pairs of vertices one can estimate the edges up to (1± ε)-error with probability 2/3, which would result in a significantly faster algorithm!
The question here is: how do different types of access to the graph result in algorithms with different complexities? Recent work by Beame, Har-Peled, Ramamoorthy, Rashtchian, and Sinha studied certain “independent set queries” and “bipartite independent set queries”: in the first (most relevant to our work), an algorithm is allowed to ask whether a set of vertices of the graph forms an independent set, and in the second, the algorithm is allowed to ask whether two sets form a bipartite independent set. The researchers give nearly matching upper and lower bounds for estimating edges with an independent set queries.
A Lower Bound on Cycle-Finding in Sparse Digraphs
Xi Chen Columbia University, Tim Randolph Columbia University, Rocco A. Servedio Columbia University, Timothy Sun Columbia University
The researchers imagined situations in which the graph is extremely large and wanted to determine whether or not the graph has cycles in a computationally efficient manner (by looking at as few of the nodes in the graph as possible). As yet, there’s no known solution to this problem that does significantly better than looking at a constant fraction of the nodes, but they proved a new lower bound – that is, they found a new limit on how efficiently the problem can be solved. In particular, their proof of the lower bound uses a new technique to capture the best possible behavior of any algorithm for this problem.
Suppose there is a large directed graph that describes the connections between neurons in a portion of the brain, and the number of neurons is very large, say, several billion. If the graph has many cycles, this might indicate that the portion of the brain contains recurrences and feedback loops, while if it has no cycles, this might indicate information flows through the graph in a linear manner. Knowing this fact might help deduce the function of this part of the brain. The paper’s result is negative – it provides a lower bound on the number of neurons needed to determine this fact. (This might sound a little discouraging, but this research isn’t really targeted at specific applications – rather, it takes a step toward better understanding the types of approaches we need to use to efficiently determine the properties of large directed graphs.)
This is part of a subfield of theoretical computer science that has to do with finding things out about enormous data objects by asking just a few questions (relatively speaking). Said Tim Randolph, “Problems like these become increasingly important as we generate huge volumes of data, because without knowing how to solve them we can’t take advantage of what we know.”
Lower Bounds for Oblivious Near-Neighbor Search
Kasper Green Larsen Aarhus University, Tal Malkin Columbia University, Omri Weinstein Columbia University, Kevin Yeo Google
The paper studies the problem of privacy-preserving (approximate) similarity search, which is the backbone of many industry-scale applications and machine learning algorithms. It obtains a quadratic improvement over the highest *unconditional* lower bound for oblivious (secure) near-neighbor search in dynamic settings. This shows that dynamic similarity search has a logarithmic price if one wishes to perform it in an (information theoretic) secure manner.
A Face Cover Perspective to $\ell_1$ Embeddings of Planar Graphs
Arnold Filtser Columbia University
In this paper the researcher studied the case where there is a set K of terminals, and the goal is to embed only the terminals into `1 with low distortion.
Given two metric spaces $(X,d_X),(Y,d_Y)$, an embedding is a function $f:X\to Y$. We say that an embedding $f$ has distortion $t$ if for every two points $u,v\in X$, it holds that $d_X(u,v)\le d_Y(f(u),f(v))\le t\cdot d_X(u,v)$. “Given a hard problem in a space $X$, it is often useful to embed it into a simpler space $Y$, solve the problem there, and then pull the solution back to the original space $X$,” said Arnold Filtser, a postdoctoral fellow. “The quality of the received solution will usually depend on the quality of the embedding (distortion), and the simplicity of the host space. Metric embeddings have a fundamental place in the algorithmic toolbox.”
In $\ell_1$ distance, a.k.a. Manhattan distance, given two vectors $\vec{x},\vec{y}\in\mathbb{R}^d$ the distance defined as $\Vert \vec{x}-\vec{y}\Vert_1=\sum_i |x_i-y_i|$. A planar graph $G=(V,E,w)$, is a graph that can be drawn in the plane in such a way that its edges $E$ intersect only at their endpoints. This paper studies metric embeddings of planar graphs into $\ell_1$.
It was conjectured by Gupta et al. that every planar graph can be embedded into $\ell_1$ with constant distortion. However, given an $n$-vertex weighted planar graph, the best upper bound on the distortion is only $O(\sqrt{\log n})$, by Rao. The only known lower bound is $2$’ and the fundamental question of the right bound is quite eluding.
The paper studies the case where there is a set $K$ of terminals, and the goal is to embed only the terminals into $\ell_1$ with low distortion and it’s contribution is a further improvement on the upper bound to $O(\sqrt{\log\gamma})$. Since every planar graph has at most $O(n)$ faces, any further improvement on this result, will be a major breakthrough, directly improving upon Rao’s long standing upper bound.
It is well known that the flow-cut gap equals to the distortion of the best embedding into $\ell_1$. Therefore, our result provides a polynomial time $O(\sqrt{\log \gamma})$-approximation to the sparsest cut problem on planar graphs, for the case where all the demand pairs can be covered by $\gamma$ faces.
Approximating the Distance to Monotonicity of Boolean Functions
Ramesh Krishnan Pallavoor Boston University, Sofya Raskhodnikova Boston University, Erik Waingarten Columbia University
A Boolean function f : {0,1}n → {0,1} is monotone if for every two points x, y ∈ {0,1}n where xi ≤ yi for every i∈[n], f(x) ≤ f(y). There has been a long and very fruitful line of research, starting with the work of Goldreich, Goldwasser, Lehman, Ron, and Samorodnitsky, exploring algorithms which can test whether a Boolean function is monotone.
The core question studied in the first paper was: suppose a function f is ϵ-far from monotone, i.e., any monotone function must differ with f on at least an ϵ-fraction of the points, how many pairs of points x, y ∈ {0,1}n which differ in only one bit i∈[n] (an edge of the hypercube) must satisfy f(x) = 1 but f(y) = 0 but x ≤ y (a violation of monotonicity)?
The paper focuses on the question of efficient algorithms which can estimate the distance to monotonicity of a function, i.e., the smallest possible ϵ where f is ϵ-far from monotone. It gives a non-adaptive algorithm making poly(n) queries which estimates ϵ up to a factor of Õ(√n). “The above approximation is not good since it degrades very badly as the number of variables of the function increases,” said Erik Waingarten. “However, the surprising thing is that substantially better approximations require exponentially many non-adaptive queries.”
The Complexity of Contracts
Paul Duetting London School of Economics, Tim Roughgarden Columbia University, Inbal Talgam-Cohen Technion, Israel Institute of Technology
Contract theory is a major topic in economics (e.g., the 2016 Nobel Prize in Economics was awarded to Oliver Hart and Bengt Holmström for their work on the topic). A canonical problem in the area is how to structure compensation to employees (e.g. as a function of sales), when the effort exerted by employees is not directly observable.
This paper provides both positive and negative results about when optimal or approximately optimal contracts can be computed efficiently by an algorithm. The researchers design such an efficient algorithm for settings with very large outcome spaces (such as all subsets of a set of products) and small agent action spaces (such as exerting low, medium, or high effort).
How to Store a Random Walk
Emanuele Viola Northeastern University, Omri Weinstein Columbia University, Huacheng Yu Harvard University
Motivated by storage applications, the researchers studied the problem of “locally-decodable” data compression. For example, suppose an encoder wishes to store a collection of n *correlated* files using as little space as possible, such that each individual X_i can be recovered quickly with few (ideally constant) memory accesses.
A natural example is a collection of similar images or DNA strands on a large sever, say, Dropbox. The researchers show that for file collections with “time-decaying” correlations (i.e., Markov chains), one can get the best of both worlds. This surprising result is achieved by proving that a random walk on any graph can be stored very close to its entropy, while still enabling *constant* time decoding on a word-RAM. The data structures generalize to dynamic (online) setting.
Labelings vs. Embeddings: On Distributed Representations of Distances
Arnold Filtser Columbia University, Lee-Ad Gottlieb Ariel University, Robert Krauthgamer Weizmann Institute of Science
The paper investigates for which metric spaces the performance of distance labeling and of `∞- embeddings differ, and how significant can this difference be.
A distance labeling is a distributed representation of distances in a metric space $(X,d)$, where each point $x\in X$ is assigned a succinct label, such that the distance between any two points $x,y \in X$ can be approximated given only their labels.
A highly structured special case is an embedding into $\ell_\infty$, where each point $x\in X$ is assigned a vector $f(x)$ such that $\|f(x)-f(y)\|_\infty$ is approximately $d(x,y)$. The performance of a distance labeling, or an $\ell_\infty$-embedding, is measured by its distortion and its label-size/dimension. “As $\ell_\infty$ is a norm space, it posses a natural structure that can be exploited by various algorithms,” said Arnold Filtser. “Thus it is more desirable to obtain embeddings rather than general labeling schemes.”
The researchers also studied the analogous question for the prioritized versions of these two measures. Here, a priority order $\pi=(x_1,\dots,x_n)$ of the point set $X$ is given, and higher-priority points should have shorter labels. Formally, a distance labeling has prioritized label-size $\alpha(.)$ if every $x_j$ has label size at most $\alpha(j)$. Similarly, an embedding $f: X \to \ell_\infty$ has prioritized dimension $\alpha(\cdot)$ if $f(x_j)$ is non-zero only in the first $\alpha(j)$ coordinates. In addition, they compare these prioritized measures to their classical (worst-case) versions.
They answer these questions in several scenarios, uncovering a surprisingly diverse range of behaviors. First, in some cases labelings and embeddings have very similar worst-case performance, but in other cases there is a huge disparity. However in the prioritized setting, they found a strict separation between the performance of labelings and embeddings. And finally, when comparing the classical and prioritized settings, they found that the worst-case bound for label size often “translates” to a prioritized one, but also a surprising exception to this rule.
Four Papers from the Theory Group Accepted to FOCS 2019
Papers from CS researchers were accepted to the 60th Annual Symposium on Foundations of Computer Science (FOCS 2019). The papers delve into population recovery, sublinear time, auctions, and graphs.
Finding Monotone Patterns in Sublinear Time
Omri Ben-Eliezer Tel-Aviv University, Clement L. Canonne Stanford University, Shoham Letzter ETH-ITS, ETH Zurich, Erik Waingarten Columbia University
The paper is about finding increasing subsequences in an array in sublinear time. Imagine an array of n numbers where at least 1% of the numbers can be arranged into increasing subsequences of length k. We want to pick random locations from the array in order to find an increasing subsequence of length k. At a high level, in an array with many increasing subsequences, the task is to find one. The key is to cleverly design the distribution over random locations to minimize the number of locations needed.
Roughly speaking, the arrays considered have a lot of increasing subsequences of length k; think of these as “evidence of existence of increasing subsequences”. However, these subsequences can be hidden throughout the array: they can be spread out, or concentrated in particular sections, or they can even have very large gaps between the starts and the ends of the subsequences.
“The surprising thing is that after a specific (and simple!) re-ordering of the “evidence”, structure emerges within the increasing subsequences of length k,” said Erik Waingarten, a PhD student. “This allows for design efficient sampling procedures which are optimal for non-adaptive algorithms.”
Beyond Trace Reconstruction: Population Recovery From the Deletion Channel
Frank Ban UC Berkeley, Xi Chen Columbia University, Adam Freilich Columbia University, Rocco A. Servedio Columbia University, Sandip Sinha Columbia University
Consider the problem of reconstructing the DNA sequence of an extinct species, given some DNA sequences of its descendant(s) that are alive today. We know that DNA sequences get modified through random mutations, which can be substitutions, insertions and deletions.
A mathematical abstraction of this problem is to recover an unknown source string x of length n, given access to independent samples of x that have been corrupted according to a certain noise model. The goal is to determine the minimum number of samples required in order to recover x with high confidence. In the special case that the corruption occurs via a deletion channel (i.e., each character in x is deleted independently with some probability, say 0.1, and the surviving characters are concatenated and transmitted), each sample is called a trace. The corresponding recovery problem is called trace reconstruction, and it has received significant attention in recent years.
The researchers considered a generalized version of this problem (known as population recovery) where there are multiple unknown source strings, along with an unknown distribution over them specifying the relative frequency of each source string. Each sample is generated by first drawing a source string with the associated probability, and then generating a trace from it via the deletion channel. The goal is to recover the source strings, along with the distribution over them (up to small error), from the mixture of traces.
For the main sample complexity upper bound, they show that for any population size s = o(log n / log log n), a population of s strings from {0,1}^n can be learned under deletion channel noise using exp(n^{1/2 + o(1)}) samples. On the lower bound side, we show that at least n^{\Omega(s)} samples are required to perform population recovery under the deletion channel when the population size is s, for all s <= n^0.49.
“I found it interesting that our work is based on certain mathematical results in which, at first glance, seem to be completely unrelated to the computational problem we consider,” said Sandip Sinha, a PhD student. In particular, they used constructions based on Chebyshev polynomials, a certain sequence of polynomials which are extremal for many properties, and is hence ubiquitous throughout theoretical computer science. Similarly, previous work on trace reconstruction rely on certain extremal results about complex-valued polynomials. Continued Sinha, “I think it is quite intriguing that complex analytic techniques yield useful results about a problem which is fundamentally about discrete structures (binary strings).”
Settling the Communication Complexity of Combinatorial Auctions with Two Subadditive Buyers
Tomer Ezra Tel Aviv University, Michal Feldman Tel Aviv University, Eric Neyman Columbia University, Inbal Talgam-Cohen Technion; S. Matthew Weinberg Princeton University
The paper is about the theory of combinatorial auctions. In a combinatorial auction, an auctioneer wants to allocate several items among bidders. Each bidder has a certain amount that they value each item; bidders also have values for combinations of items, and in a combinatorial auction a bidder might not value a combination of items as much as each item individually.
For instance, say that a pencil and a pen will be auctioned. The pencil is valued at 30 cents and the pen at 40 cents, but the pen and pencil together at only 50 cents (it may be that there isn’t any additional value from having both the pencil and the pen). Valuation functions with this property — that the value of a combination of items is less than or equal to the sum of the values of each item — are called subadditive.
In the paper, the researchers answered a longstanding open question about combinatorial auctions with two bidders who have subadditive valuation — roughly speaking, is it possible for an auctioneer to efficiently communicate with both bidders to figure out how to allocate the items between them to make the bidders happy?
The answer turns out to be no. In general, if the auctioneer wants to do better than just giving all of the items to one bidder or the other at random, the auctioneer needs to communicate a very large amount with the bidders.
The result itself was somewhat surprising, the researchers expected it to be possible for the auctioneer to do pretty well without having to communicate with the bidders too much. “Also, information theory was extensively used as part of proving the result,” said Eric Neyman, a PhD student. “This is unexpected, because information theory has not been used much in the study of combinatorial auctions.”
Fully Dynamic Maximal Independent Set with Polylogarithmic Update Time
Soheil Behnezhad University of Maryland, Mahsa Derakhshan University of Maryland, Mohammad Taghi Hajiaghayi University of Maryland, Cliff Stein Columbia University, Madhu Sudan Harvard University
In a graph, an independent set is a set of vertices with the property that none are adjacent. For example, in the graph of Facebook friends, vertices are people and there is an edge between two people who are friends. An independent set would be a set of people, none of whom are friends with each other. A basic problem is to find a large independent set. The paper focuses on one type of large independent set known as a maximal independent set, that is, one that cannot have any more vertices added to it.
Graphs, such as the friends graph, evolve over time. As the graph evolves, the maximal independent set needs to be maintained, without recomputing one from scratch. The paper significantly decreases the time to do so, from time that is polynomial in the input size to one that is polylogarithmic.
A graph can have many maximal independent sets (e.g. in a triangle, each of the vertices is a potential maximal independent set). One might think that this freedom makes the problems easier. The researchers picked one particular kind of maximal independent set, known as a lexicographically first maximal independent set (roughly this means that in case of a tie, the vertex whose name is first in alphabetical order is always chosen) and show that this kind of set can be maintained more efficiently.
“Giving up this freedom actually makes the problems easier,” said Cliff Stein, a computer science professor. “The idea of restricting the set of possible solutions making the problem easier is a good general lesson.”