Google Research held an online workshop on the conceptual understanding of deep learning. The workshop discussed how new findings in deep learning and neuroscience can help create better artificial intelligence systems. Christos Papadimitriou discussed how our growing understanding of information-processing mechanisms in the brain might help create algorithms that are more robust in understanding and engaging in conversations. Papadimitriou presented a simple and efficient model that explains how different areas of the brain inter-communicate to solve cognitive problems.
Edge-Weighted Online Bipartite Matching Matthew Fahrbach Google Research, Zhiyi Huang University of Hong Kong, Runzhou Tao Columbia University, Morteza Zadimoghaddam Google Research
The online bipartite matching problem introduced by Richard Karp, Umesh Vazirani, and Vijay Vazirani in 1990 is one of the most important problems in the field of online algorithms. In this problem, only one side of the bipartite graph (called “offline nodes”) is given. The other side of the graph (called “online nodes”) is given one by one. Each time an online node arrives, the algorithm must decide whether and how it should be matched. This decision is irrevocable. The online bipartite matching problem has a wide range of applications, e.g., online ad allocation, in which we can see advertisers as offline nodes and users as online nodes.
This paper gives a positive answer for this 30-year open problem by giving an 0.508-competitive algorithm for the edge-weighted bipartite online matching problem. The algorithm uses a new subroutine called Online Correlated Selection, which takes a sequence of pairs as input and selects one element from each pair. By negatively correlating the selections, one can produce a better online matching algorithm.
This new technique will have further applications in the field of online algorithms.
Consider the problem of maintaining a directed graph under edge addition/deletions, so that connectivity between any pair of vertices can be answered quickly. This basic problem has no efficient data structure, despite decades of research. In 2010, Patrascu proposed a communication problem (the “Multiphase Conjecture”), whose resolution would prove that problems like dynamic reachability indeed require slow (n^0.1) update or query time. We use information-theoretic tools to prove a weaker version of the Multiphase Conjecture, which implies a polynomial (~ \sqrt{n}) lower bound on “weakly-adaptive” dynamic data structures for the reachability problem. We also use this result to make progress on understanding the power of nonlinear gates in networks computing *linear* operators (x –> Ax).
This paper resolves an open question about the complexity of estimating the edit distance up to a constant factor. Edit distance is a fundamental problem, and its exact quadratic-time algorithm is one of the most classic dynamic programming problems.
It was shown that under the SETH conjecture, no exact algorithm can resolve it in sub-quadratic, so the open question remained what is the best approximation one can obtain. A breakthrough result from 2018 showed the first trust sub-quadratic algorithm for Constant factor, and the question remained if it can be done in near-linear time. This paper resolved this question positively.
Range-counting is one of the most omnipresent query spatial databases, computational geometry, and eCommerce (e.g. “Find all employees from countries X who have earned salary >X between years 2000-2018”). Fast data structures with linear space are known for various such problems, all of which use only additions and subtractions of pre-computed weighted sums (aka the “group model”). However, for general ranges (geometric shapes), no efficient data structures were known, yet proving > log(n)
Lower bounds in the group model remained a fundamental challenge since the early 1980s. The paper proves a *polynomial* (n^0.1) lower bound on the query time of linear-space data structures for an explicit range-counting problem of convex polygons in R^2.
Fundamental routing problems such as the Traveling Salesman Problem (TSP) and the Vehicle Routing Problem have been widely studied since the 1950s. Given a metric space, the goal is to find a minimum-weight collection of tours (only one for TSP) so as to meet a prescribed demand at some points of the metric space. Both problems have been the source of inspiration for many algorithmic breakthroughs and, quite frustratingly, remain good examples of the limits of the power of algorithmic methods.
The paper studies the geometry of weighted minor free graphs, which is a generalization of planar graphs, where the graph is somewhat topologically restricted. The framework is this of metric embeddings, where we create a “small-complexity” graph that approximately preserves distances between pairs of points in the original graph. We have two such structural results:
1. Light subset spanner: given a set K of terminals, we construct a subgraph of the original graph that preserves all distances between terminals up to 1+\eps factor and have total weight only slightly larger than the Steiner tree: the minimal weight subgraph connecting all terminals.
2. Stochastic metric embedding into low treewidth graphs: treewidth is a graph parameter measuring how much a graph is “treelike”. Many hard problems become tractable on bounded treewidth graphs. We create a distribution over mapping of the graph into a bounded treewidth graph, such that the distance between every pair of points increases only by a small additive constant (in expectation).
The structural results are then used to obtain an efficient polynomial approximation scheme (EPTAS) for subset TSP in minor-free graphs, and a quasi-polynomial approximation scheme (QPTAS) for the vehicle routing problem in minor-free graphs.
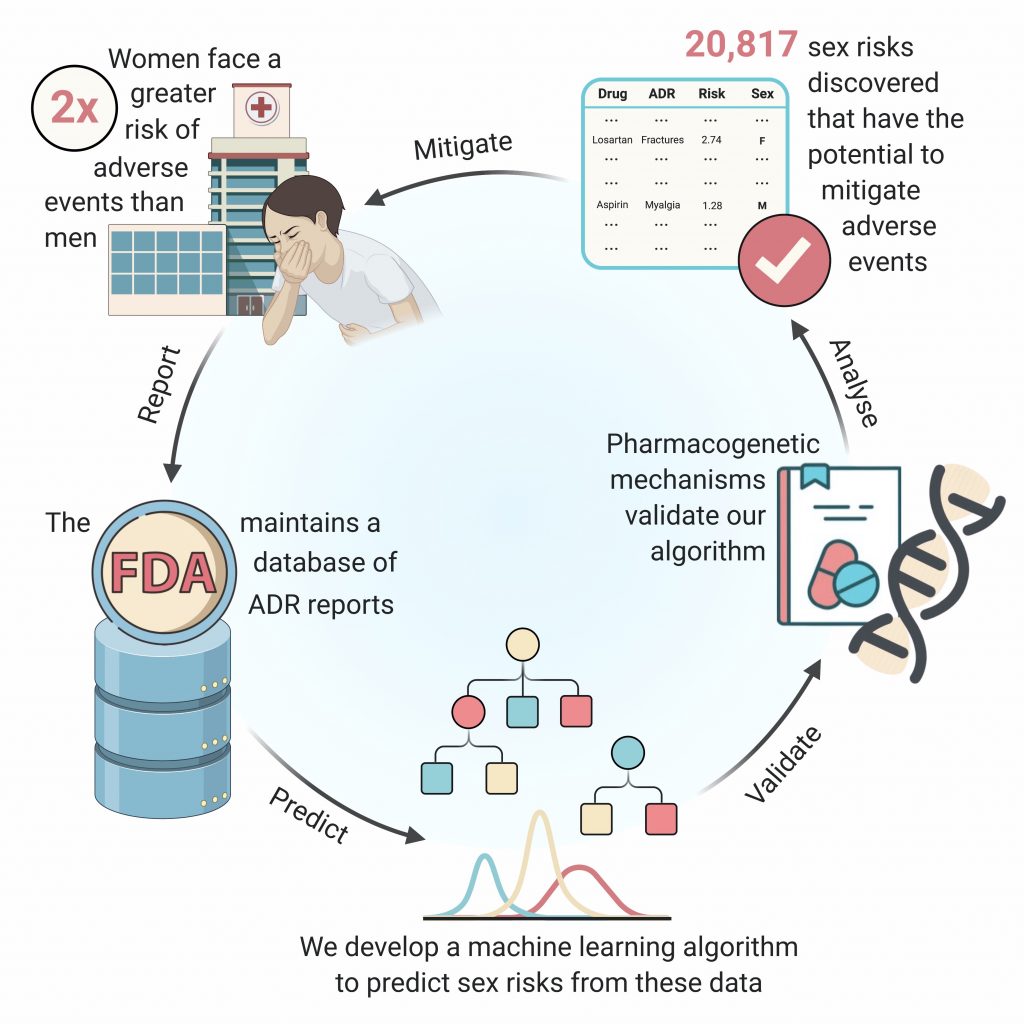
Payal Chandak (CC ’21) developed a machine learning model, AwareDX, that helps detect adverse drug effects specific to women patients. AwareDX mitigates sex biases in a drug safety dataset maintained by the FDA.
Below, Chandak talks about how her internship under the guidance of Nicholas Tatonetti, associate professor of biomedical informatics and a member of the Data Science Institute, inspired her to develop a machine learning tool to improve healthcare for women.
Payal Chandak
How did the project come about? I initiated this project during my internship at the Tatonetti Lab (T-lab) the summer after my first year. T-lab uses data science to study the side effects of drugs. I did some background research and learned that women face a two-fold greater risk of adverse events compared to men. While knowledge of sex differences in drug response is critical to drug prescription, there currently isn’t a comprehensive understanding of these differences. Dr. Tatonetti and I felt that we could use machine learning to tackle this problem and that’s how the project was born.
How many hours did you work on the project? How long did it last? The project lasted about two years. We refined our machine learning (ML) model, AwareDX, over many iterations to make it less susceptible to biases in the data. I probably spent a ridiculous number of hours developing it but the journey has been well worth it.
Were you prepared to work on it or did you learn as the project progressed? As a first-year student, I definitely didn’t know much when I started. Learning on the go became the norm. I understood some things by taking relevant CS classes and through reading Medium blogs and GitHub repositories –– this ability to learn independently might be one of the most valuable skills I have gained. I am very fortunate that Dr. Tatonetti guided me through this process and invested his time in developing my knowledge.
What were the things you already knew and what were the things you had to learn while working on the project? While I was familiar with biology and mathematics, computer science was totally new! In fact, T-Lab launched my journey to exploring computer science. This project exposed me to the great potential of artificial intelligence (AI) for revolutionizing healthcare, which in turn inspired me to explore the discipline academically. I went back and forth between taking classes relevant to my research and applying what I learned in class to my research. As I took increasingly technical classes like ML and probabilistic modelling, I was able to advance my abilities.
Looking back, what were the skills that you wished you had before the project? Having some experience with implementing real-world machine learning projects on giant datasets with millions of observations would have been very valuable.
Was this your first project to collaborate on? How was it? This was my first project and I worked under the guidance of Dr. Tatonetti. I thought it was a wonderful experience – not only has it been extremely rewarding to see my work come to fruition, but the journey itself has been so valuable. And Dr. Tatonetti has been the best mentor that I could have asked for!
Did working on this project make you change your research interests? I actually started off as pre-med. I was fascinated by the idea that “intelligent machines” could be used to improve medicine, and so I joined T-Lab. Over time, I’ve realized that recent advances in machine learning could redefine how doctors interact with their patients. These technologies have an incredible potential to assist with diagnosis, identify medical errors, and even recommend treatments. My perspective on how I could contribute to healthcare shifted completely, and I decided that bioinformatics has more potential to change the practice of medicine than a single doctor will ever have. This is why I’m now hoping to pursue a PhD in Biomedical Informatics.
Do you think your skills were enhanced by working on the project? Both my knowledge of ML and statistics and my ability to implement my ideas have grown immensely as a result of working on this project. Also, I failed about seven times over two years. We were designing the algorithm and it was an iterative process – the initial versions of the algorithm had many flaws and we started from scratch multiple times. The entire process required a lot of patience and persistence since it took over 2 years! So, I guess it has taught me immense patience and persistence.
Why did you decide to intern at the T-Lab? I was curious to learn more about the intersection of artificial intelligence and healthcare. I’m endlessly fascinated by the idea of improving the standards of healthcare by using machine learning models to assist doctors.
Would you recommend volunteering or seeking projects out to other students? Absolutely. I think everyone should explore research. We have incredible labs here at Columbia with the world’s best minds leading them. Research opens the doors to work closely with them. It creates an environment for students to learn about a niche discipline and to apply the knowledge they gain in class.
The Symposium on Theory of Computing (STOC) covers research within theoretical computer science, such as algorithms and computation theory. This year, four papers from CS researchers and collaborators from various institutions made it into the conference.
The researchers were interested in the problem of compressing texts with local context, like texts in which there is some correlation between nearby characters. For example, the letter ‘q’ is almost always followed by ‘u’ in an English text.
It is a reasonable goal to design compression schemes that exploit local context to reduce the length of the string considerably. Indeed, the FM-Index and other such schemes, based on a transformation called the Burrows-Wheeler transform followed by Move-to-Front encoding, have been widely used in practice to compress DNA sequences etc. “I think it’s interesting that compression schemes have been known for nearly 20 years in the pattern-matching and bioinformatics community but there has not been satisfactory theoretical guarantees of the compression achieved by these algorithms,” said Sandip Sinha, a PhD student in the Theory Group.
Moreover, these schemes are inherently non-local – in order to extract a character or a short substring at a particular position of the original text, one needs to decode the entire string, which requires time proportional to the length of the original string. This is prohibitive in many applications. The team designed a data structure which matches almost exactly the space bound of such compression schemes, while also supporting highly efficient local decoding queries (alluded to above), as well as certain pattern-matching queries. In particular, they were able to design a succinct “locally-decodable” Move-to-Front (MTF) code, that reduces the decoding time per character (in the MTF encoding) from n to around log(n), where n is the length of the string. Shared Sinha, “We also show a lower bound showing that for a wide class of strings, one cannot hope to do much better using any data structure based on the above transform.”
“Hopefully our paper draws wider attention of the theoretical CS community to similar problems in these fields,” said Sinha. To that end, they have made a conscious effort to make the paper accessible across research domains. “I also think there is no significant mathematical knowledge required to understand the paper, beyond some basic notions in information theory.”
Fooling Polytopes Ryan O’Donnell Carnegie Mellon University, Rocco A. Servedio Columbia University, Li-Yang Tan Stanford University
The paper is about “getting rid of the randomness in random sampling”.
Suppose you are given a complicated shape on a blackboard and you need to estimate what fraction of the blackboard’s area is covered by the shape. One efficient way to estimate this fraction is by doing random sampling: throw darts randomly at the blackboard and count the fraction of the darts that land inside the shape. If you throw a reasonable number of darts, and they land uniformly at random inside the blackboard, the fraction of darts that land inside the shape will be a good estimate of the actual fraction of the blackboard’s area that is contained inside the shape. (This is analogous to surveying a small random sample of voters to try and predict who will win an election.)
“This kind of random sampling approach is very powerful,” said Rocco Servedio, professor and chair of the computer science department. “In fact, there is a sense in which every randomized computation can be viewed as doing this sort of random sampling.”
It is a fundamental goal in theoretical computer science to understand whether randomness is really necessary to carry out computations efficiently. The point of this paper is to show that for an important class of high-dimensional estimation problems of the sort described above, it is actually possible to come up with the desired estimates efficiently without using any randomness at all.
In this specific paper, the “blackboard” is a high-dimensional Boolean hypercube and the “shape on the blackboard” is a subset of the hypercube defined by a system of high-dimensional linear inequalities (such a subset is also known as a polytope). Previous work had tried to prove this result but could only handle certain specialized types of linear inequalities. By developing some new tools in high dimensional geometry and probability, in this paper the researchers were able to get rid of those limitations and handle all systems of linear inequalities.
The paper shows an interesting connection between the task of proving time-space lower bounds on data structure problems (with linear queries), and the long-standing open problem of constructing “stable” (rigid) matrices — a matrix M whose rank remains very high unless a lot of entries are modified. Constructing rigid matrices is one of the major open problems in theoretical computer science since the late 1970s, with far-reaching consequences on circuit complexity.
The result shows a real barrier for proving lower bounds on data structures: If one can exhibit any “hard” data structure problem with linear queries (the canonical example being Range Counting queries: given n points in d dimensions, report the number of points in a given rectangle), then this problem can be essentially used to construct “stable” (rigid) matrices.
“This is a rather surprising ‘threshold’ result, since in slightly weaker models of data structures (with small space usage), we do in fact have very strong lower bounds on the query time,” said Omri Weinstein, an assistant professor of computer science. “Perhaps surprisingly, our work shows that anything beyond that is out of reach with current techniques.”
The paper is about testing unateness of Boolean functions on the hypercube.
For this paper the researchers set out to design highly efficient algorithms which, by evaluating very few random inputs of a Boolean function, can “test” whether the function is unate (meaning that every variable is either non-increasing or non-decreasing or is pretty non-unate).
Referring to a previous paper the researchers set out to create an algorithm which is optimal (up to poly-logarithmic factors), giving a lower bound on the complexity of these testing algorithms.
An example of a Boolean function which is unate is a halfspace, i.e., for some values w1, …, wn, θ ∈ ℝ, the function f : {0,1}n → {0,1} is given by f(x) = 1 if ∑ wi xi≥ θ and 0 otherwise. Here, every variable i ∈ [n] is either non-decreasing, when wi ≥ 0, or non-increasing, when wi ≤ 0.
“One may hope that such an optimal algorithm could be non-adaptive, in the sense that all evaluations could be done at once,” said Erik Waingarten, an algorithms and computational complexity PhD student. “These algorithms tend to be easier to analyze and have the added benefit of being parallelize-able.”
However, the algorithm they developed is crucially adaptive, and a surprising thing is that non-adaptive algorithms could never achieve optimal complexity. A highlight of the paper is a new analysis of a very simple binary search procedure on the hypercube.
“This procedure is the ‘obvious’ thing one would do for these kinds of algorithms, but analyzing it has been very difficult because of its adaptive nature,” said Waingarten. “For us, this is the crucial component of the algorithm.”
Four papers were accepted to the Foundations of Computer Science (FOCS) symposium. CS researchers worked alongside colleagues from various organizations to develop the algorithms.
Authors: Anindya De Northwestern University, Philip M. Long Google, Rocco Servedio Columbia University
The paper is about a new algorithm for learning an unknown probability distribution given draws from the distribution.
A simple example of the problem that the paper considers can be illustrated with a penny tossing scenario: Suppose you have a huge jar of pennies, each of which may have a different probability of coming up heads. If you toss all the pennies in the jar, you’ll get some number of heads; how many times do you need to toss all the pennies before you can build a highly accurate model of how many pennies are likely to come up heads each time? Previous work answered this question, giving a highly efficient algorithm to learn this kind of probability distribution.
The current work studies a more difficult scenario, where there can be several different kinds of coins in the jar — for example, it may contain pennies, nickels and quarters. Each time you toss all the coins, you are told the total *value* of the coins that came up heads (but not how many of each type of coin came up heads).
“Something that surprised me is that when we go from only one kind of coin to two kinds of coins, the problem doesn’t get any harder,” said Rocco Servedio, a researcher from Columbia University. “There are algorithms which are basically just as efficient to solve the two-coin problem as the one-coin problem. But we proved that when we go from two to three kinds of coins, the problem provably gets much harder to solve.”
Authors: Alexandr Andoni Columbia University, Assaf Naor Princeton University, Aleksandar Nikolov University of Toronto, Ilya Razenshteyn Microsoft Research Redmond, Erik Waingarten Columbia University
This paper gives new algorithms for the approximate near neighbor (ANN) search problem for general normed spaces. The problem is a classic problem in computational geometry, and a way to model “similarity search”.
For example, Spotify may need to preprocess their dataset of songs so that new users may find songs which are most similar to their favorite songs. While a lot of work goes into designing good algorithms for ANN, these algorithm work for specific metric spaces of interest to measure the distance between two points (such as Euclidean or Manhattan distance). This work is the first to give non-trivial algorithms for general normed spaces.
“One thing which surprised me was that even though the embedding appears weaker than established theorems that are commonly used, such as John’s theorem, the embedding is efficiently computable and gives more control over certain parameters,” said Erik Waingarten, an algorithms and computational complexity PhD student.
Authors: Alexandr Andoni Columbia University, Zhao Song Harvard University & UT-Austin, Clifford Stein Columbia University, Zhengyu Wang Harvard University, Peilin Zhong Columbia University
This paper is about designing fast algorithms for problems on graphs in parallel systems, such as MapReduce. The latter systems have been widely-successful in practice, and invite designing new algorithms for these parallel systems. While many classic “parallel algorithms” were been designed in the 1980s and 1990s (PRAM algorithms), predating the modern massive computing clusters, they had a different parallelism in mind, and hence do not take full advantage of the new systems.
The typical example is the problem of checking connectivity in a graph: given N nodes together with some connecting edges (e.g., a friendship graph or road network), check whether there’s a path between two given nodes. The classic PRAM algorithm solves this in “parallel time” that is logarithmic in N. While already much better than the sequential-time of N (or more), the researchers considered to question whether one can do even better in the new parallel systems a-la MapReduce.
While obtaining a much better runtime seems out of reach at the moment (some conjecture impossible), the researchers realized that they may be able to obtain faster algorithms when the graphs have a small diameter, for example if any two connected nodes have a path at most 10 hops. Their algorithm obtains a parallel time that is logarithmic in the diameter. (Note that the diameter of a graph is often much smaller than N.)
“Checking connectivity may be a basic problem, but its resolution is fundamental to understanding many other problems of graphs, such as shortest paths, clustering, and others,” said Alexandr Andoni, one of the authors. “We are currently exploring these extensions.”
Authors: Marshall Ball Columbia University, Dana Dachman-Soled University of Maryland, Siyao Guo Northeastern University, Tal Malkin Columbia University, Li-Yang Tan Stanford University
With this paper, the researchers constructed new non-malleable codes that improve efficiency over what was previously known.
“With non-malleable codes, any attempt to tamper with the encoding will do nothing and what an attacker can only hope to do is replace the information with something completely independent,” said Maynard Marshall Ball, a fourth year PhD student. “That said, non-malleable codes cannot exist for arbitrary attackers.”
The constructions were derived via a novel application of a powerful circuit lower bound technique (pseudorandom switching lemmas) to non-malleability. While non-malleability against circuit classes implies strong lower bounds for those same classes, it is not clear that the converse is true in general. This work shows that certain techniques for proving strong circuit lower bounds are indeed strong enough to yield non-malleability.
Dean Boyce's statement on amicus brief filed by President Bollinger
President Bollinger announced that Columbia University along with many other academic institutions (sixteen, including all Ivy League universities) filed an amicus brief in the U.S. District Court for the Eastern District of New York challenging the Executive Order regarding immigrants from seven designated countries and refugees. Among other things, the brief asserts that “safety and security concerns can be addressed in a manner that is consistent with the values America has always stood for, including the free flow of ideas and people across borders and the welcoming of immigrants to our universities.”
This recent action provides a moment for us to collectively reflect on our community within Columbia Engineering and the importance of our commitment to maintaining an open and welcoming community for all students, faculty, researchers and administrative staff. As a School of Engineering and Applied Science, we are fortunate to attract students and faculty from diverse backgrounds, from across the country, and from around the world. It is a great benefit to be able to gather engineers and scientists of so many different perspectives and talents – all with a commitment to learning, a focus on pushing the frontiers of knowledge and discovery, and with a passion for translating our work to impact humanity.
I am proud of our community, and wish to take this opportunity to reinforce our collective commitment to maintaining an open and collegial environment. We are fortunate to have the privilege to learn from one another, and to study, work, and live together in such a dynamic and vibrant place as Columbia.
Sincerely,
Mary C. Boyce
Dean of Engineering
Morris A. and Alma Schapiro Professor
Add to GMail