Five Research Papers Accepted to FOCS 2025
Research from the department was featured at the 66th Annual Symposium on Foundations of Computer Science (FOCS 2025). Several of our faculty and students had their papers accepted, contributing new insights to areas such as algorithms, complexity theory, and cryptography. This digest provides an overview of their work and showcases the innovative research emerging from our community.
Two professors were also recognized with Test of Time Awards. Rocco Servedio was honored for his 2005 paper, Agnostically Learning Half Spaces, and Toniann Pitassi received the award for her 2015 work, Deterministic Communication vs. Partition Number.
Below are the abstracts of the accepted papers.
Faster exact learning of k-term DNFs with membership and equivalence queries
Josh Alman Columbia University, Shivam Nadimpalli (MIT), Shyamal Patel Columbia University, Rocco A. Servedio Columbia University
Abstract:
In 1992 Blum and Rudich [BR92] gave an algorithm that uses membership and equivalence queries to learn k-term DNF formulas over {0, 1} n in time poly(n, 2 k ), improving on the naive O(n k ) running time that can be achieved without membership queries [Val84]. Since then, many alternative algorithms [Bsh95, Kus97, Bsh97, BBB+00] have been given which also achieve runtime poly(n, 2 k ). We give an algorithm that uses membership and equivalence queries to learn k-term DNF formulas in time poly(n) · 2 O˜( √ k) . This is the first improvement for this problem since the original work of Blum and Rudich [BR92]. Our approach employs the Winnow2 algorithm for learning linear threshold functions over an enhanced feature space which is adaptively constructed using membership queries. It combines a strengthened version of a technique that effectively reduces the length of DNF terms from the original work of [BR92] with a range of additional algorithmic tools (attribute-efficient learning algorithms for low-weight linear threshold functions and techniques for finding relevant variables from junta testing) and analytic ingredients (extremal polynomials and noise operators) that are novel in the context of query-based DNF learning.
Embeddings into Similarity Measures for Nearest Neighbor Search
Alexandr Andoni Columbia University, Negev Shekel Nosatzki Columbia University
Abstract:
In this note, we show that one can use average embeddings, introduced recently in [Nao20], to obtain efficient algorithms for approximate nearest neighbor search. In particular, a metric X embeds into ℓ2 on average, with distortion D, if, for any distribution µ on X, the embedding is D Lipschitz and the (square of) distance does not decrease on average (wrt µ). In particular existence of such an embedding (assuming it is efficient) implies a O(D 3 ) approximate nearest neigbor search under X. This can be seen as a strengthening of the classic (bi-Lipschitz) embedding approach to nearest neighbor search, and is another application of data-dependent hashing paradigm.
Generalized Flow in Nearly-linear Time on Moderately Dense Graphs
Shunhua Jiang Columbia University, Michael Kapralov EPFL, Switzerland, Lawrence Li Er Lu University of Toronto, Aaron Sidford Stanford University
Abstract:
In this paper, we consider generalized flow problems where there is an m-edge n-node directed graph G = (V, E) and each edge e ∈ E has a loss factor γe > 0 governing whether the flow is increased or decreased as it crosses edge e. We provide a randomized Oe((m+n 1.5 )·polylog( W δ )) time algorithm for solving the generalized maximum flow and generalized minimum cost flow problems in this setting where δ is the target accuracy and W is the maximum of all costs, capacities, and loss factors and their inverses. This improves upon the previous state-of-theart Oe(m √ n · log2 ( W δ )) time algorithm, obtained by combining the algorithm of [DS08] with techniques from [LS14]. To obtain this result we provide new dynamic data structures and spectral results regarding the matrices associated to generalized flows and apply them through the interior point method framework of [vdBLL+21].
Stronger Cell Probe Lower Bounds via Local PRGs
Oliver Korten Columbia University, Toniann Pitassi Columbia University, Russell Impagliazzo University of California, San Diego
Abstract:
In this work, we observe a tight connection between three topics: NC0 cryptography, NC0 range avoidance, and static data structure lower bounds. Using this connection, we leverage techniques from the cryptanalysis of NC0 PRGs to prove state-of-the-art results in the latter two subjects. Our main result is an improvement to the best known static data structure lower bounds, breaking a barrier which has stood for several decades. Prior to our work, the best known lower bound for any explicit problem with M inputs and N queries was S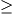 Nt1(logM)1−t1 for any setting of the word length w (where S= space and t= time) (Siegel ‘89). We prove, for the same class of explicit problems considered by Siegel, a quadratically stronger lower bound of the form S
Nt1(logM)1−t1 for any setting of the word length w (where S= space and t= time) (Siegel ‘89). We prove, for the same class of explicit problems considered by Siegel, a quadratically stronger lower bound of the form S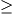
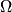

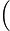 Nt2
Nt2 (logM)1−t2
(logM)1−t2 2−O(w)
2−O(w)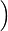 for all even t
for all even t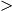 0. Second, for the restricted class of nonadaptive bit probe data structures, we improve on this lower bound polynomially: for all odd constants t
0. Second, for the restricted class of nonadaptive bit probe data structures, we improve on this lower bound polynomially: for all odd constants t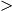 1 we give an explicit problem with N queries and M
1 we give an explicit problem with N queries and M NO(1) inputs and prove a lower bound S
NO(1) inputs and prove a lower bound S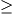
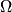 (Nt2+
(Nt2+ t) for some constant
t) for some constant  t
t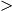 0. Our results build off of an exciting body of work on refuting semi-random CSPs.
0. Our results build off of an exciting body of work on refuting semi-random CSPs.
We then utilize our explicit cell probe lower bounds to obtain the best known unconditional algorithms for NC0 range avoidance: we can solve any instance with stretch n
 m in polynomial time once m
m in polynomial time once m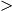
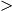 nt2 when t is even; with the aid of an NP oracle we can solve any instance with m
nt2 when t is even; with the aid of an NP oracle we can solve any instance with m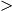 nt2−
nt2− t for
t for  t
t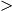 0 when t is odd. Finally, using our main correspondence we establish novel barrier results for obtaining significant improvements to our cell probe lower bounds: (i) near-optimal space lower bounds for an explicit problem with t=4
0 when t is odd. Finally, using our main correspondence we establish novel barrier results for obtaining significant improvements to our cell probe lower bounds: (i) near-optimal space lower bounds for an explicit problem with t=4 w=1 implies EXPNP
w=1 implies EXPNP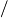
 NC1 ; (ii) under the widely-believed assumption that polynomial-stretch NC0 PRGs exist, there is no natural proof of a lower bound of the form S
NC1 ; (ii) under the widely-believed assumption that polynomial-stretch NC0 PRGs exist, there is no natural proof of a lower bound of the form S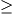 N
N (1) when t=
(1) when t=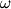 (1), w=1.
(1), w=1.
Kronecker Powers, Orthogonal Vectors, and the Asymptotic Spectrum
Josh Alman Columbia University, Baitian Li Tsinghua University
Abstract:
We study circuits for computing linear transforms defined by Kronecker power matrices. The best-known (unbounded-depth) circuits, including the widely-applied fast Walsh–Hadamard transform and Yates’ algorithm, can be derived from the best-known depth-2 circuits using known constructions, so we focus particularly on the depth-2 case. Recent work [JS13, Alm21, AGP23, Ser22] has improved on decades-old constructions in this area using a new rebalancing approach, but it was unclear how to apply this approach optimally, and the previous versions had complicated technical requirements.
We find that Strassen’s theory of asymptotic spectra can be applied to capture the design of these circuits. This theory was designed to generalize the known techniques behind matrix multiplication algorithms as well as a variety of other algorithms with recursive structure, and it brings a number of new tools to use for designing depth-2 circuits. In particular, in hindsight, we find that the techniques of recent work on rebalancing were proving special cases of the duality theorem which is central to Strassen’s theory. We carefully outline a collection of obstructions to designing small depth-2 circuits using a rebalancing approach, and apply Strassen’s theory to show that our obstructions are complete.
Using this connection, combined with other algorithmic techniques (including matrix rigidity upper bounds, constant-weight binary codes, and a “hole-fixing lemma” from recent matrix multiplication algorithms), we give new improved circuit constructions as well as other applications, including:
• The N ×N disjointness matrix has a depth-2 linear circuit of size O(N 1.2495) over any field. This is the first construction which surpasses exponent 1.25, and thus yields smaller circuits for many families of matrices using reductions to disjointness, including all Kronecker products of 2 × 2 matrices, without using matrix rigidity upper bounds.
• Barriers to further improvements, including that the Strong Exponential Time Hypothesis implies an N1+Ω(1) size lower bound for depth-2 linear circuits computing the Walsh– Hadamard transform (and the disjointness matrix with a technical caveat), and that proving such a N1+Ω(1) depth-2 size lower bound would imply breakthrough threshold circuit lower bounds.
• The Orthogonal Vectors (OV) problem in moderate dimension d can be solved in deterministic time O˜(n · 1.155d ), derandomizing an algorithm of Nederlof and Węgrzycki [NW21], and the counting problem can be solved in time O˜(n · 1.26d ), improving an algorithm of Williams [Wil24] which runs in time O˜(n · 1.35d ). We design these new algorithms by noticing that prior algorithms for OV can be viewed as corresponding to depth-2 circuits for the disjointness matrix, then using our framework for further improvements.

