Interview with Xi Chen, coauthor of Complexity Dichotomies for Counting Problems

A counting problem asks the question: What is the exact number of solutions that exist for a given instance of a computational problem?

Theoretical computer scientists in the last 15 years have made tremendous progress in understanding the complexity of several families of counting problems, resulting in a number of intriguing dichotomies: a problem in each family is either easy—solvable in polynomial time—or computationally hard. Complexity Dichotomies for Counting Problems, Volume 1, Boolean Domain, a new book by Jin-Yi Cai (University of Wisconsin, Madison) and Xi Chen, provides a high-level overview of the current state of dichotomies for counting problems, pulling together and summarizing the major results and key papers that have contributed to progress in the field. This is the first time much of this material is available in book form.

Structured around several families of problems—counting constraint specification problems (#CSP), Holant, counting graph homomorphisms—the book begins by introducing many common techniques that are reused in later proofs. Each subsequent chapter revolves around a family of problems, starting with easier, specific cases before moving onto more complex and more general cases.

For the first volume, the authors focus on the Boolean domain (where variables are assigned 0-1 values); a second volume, expected to be released next year, will look at problems in the general domain where variables can be assigned three, four, or any number of values.

In this interview, Chen talks more about the motivation for the book and why dichotomies for counting problems is an area deserving of more study.

Why write the book?

Currently it’s hard for PhD students and others to get started in the field. Many of the papers are long and technically very dense, and they build on work done in previous papers. To understand one paper often requires a lot of backtracking. This can be frustrating at times because different papers use different notation and sometimes prove the same result or use the same tool in different contexts.

Our aim in writing this book was to minimize the effort needed to study dichotomies for counting problems. We summarize and streamline the major results using a common notation and unified framework so it is easier to see the progression of ideas and techniques. To encourage students to start working in this area, we wrote the book so an undergraduate with some basic knowledge of complexity theory can follow the proofs.

Could you define at a high level “dichotomies for counting problems”?

Counting problems involve determining the exact number of solutions that exist for a given input instance. Does a 3SAT instance have 10 or 11 satisfying assignments or 20 or 27? What is the exact number? In a graph, for instance, you might want to know the exact number of ways to apply three colors to vertices so that no two adjacent vertices share the same color.

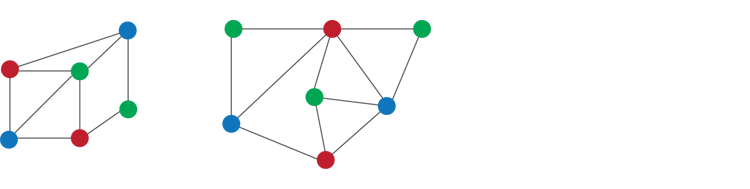
A number of families of counting problems have been studied. For example, we are interested in counting homomorphisms from an input graph G to a fixed graph H (where a homomorphism from G to H is a map f from vertices of G to vertices of H that preserves edges in G). In this case, each graph H defines a counting problem; e.g., when H is the triangle, the problem it defines is exactly the problem of counting 3-colorings. The 3-coloring problem is one of the classical problems known to be #P-hard, where #P is the complexity class that contains all counting problems, just as NP is for decision problems.

Can we classify EVERY graph H according to the complexity of the counting problem it defines? Such a result is called a dichotomy, which shows that all problems of a certain family can be classified into one of two groups: those admitting efficient algorithms and those that are #P-hard. Imagining each problem in a family as a dot, a dichotomy theorem can be viewed as a curve that classifies all the dots correctly according to their complexities. This curve typically involves a number of well-defined conditions: every problem that violates one of these conditions can be shown to be #P-hard and every problem that satisfies all the conditions can be solved by a unified efficient algorithm.

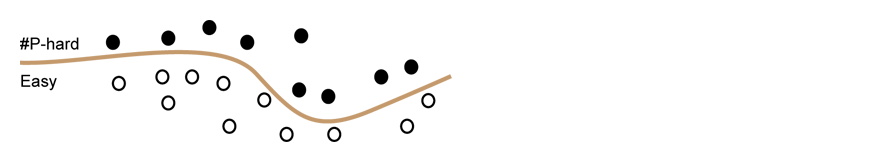
How has the field matured in the past few years?

Proofs have gotten stronger and more general. In the language of counting constraint satisfaction problems, the dichotomy theorem we had fifteen years ago only applied to problems defined by a single 0-1 valued symmetric function. In contrast we now have a full dichotomy for all counting constraint satisfaction problems (i.e., all problems defined by multiple complex-valued constraint functions with arbitrary arities).

What attracts you to the problem?

To me it is amazing that for these families of problems, a dichotomy theorem exists to once and for all classify the complexity of every problem. As it is shown by the classical Ladner’s theorem, there are infinitely many layers of problems in #P, ordered by their complexity, between P and #P-hard problems. Every time you move outside by one layer, problems become strictly harder.

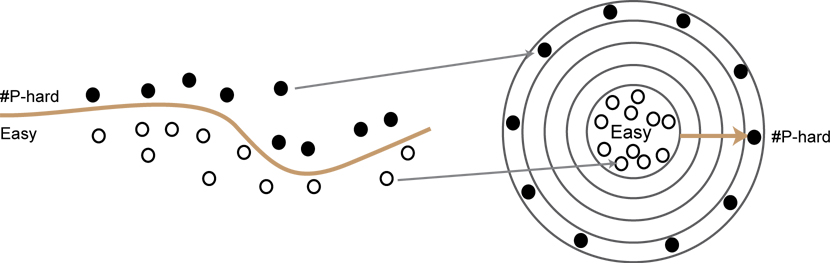
Dichotomy theorems covered in the book, however, show that all (infinitely many) problems in these lie either in P (the core) or the outmost #P-hard shell, and none of them belongs to layers in between. The intuition to me is that these families consist of “natural” counting problems only and do not contain any of those strange “#P-intermediate” problems, but I am curious: how much further can we go as we move to more and more general families of counting problems? Especially with Holant problems, not much is known for the general domain case. It’s one reason we need to develop stronger techniques to prove dichotomies for more general families of counting problems.

Volume 2 of Complexity Dichotomies for Counting Problems, which covers the general domain, is expected to be published next year.

Posted 02/21/18