In discrete choice modeling, estimating parameters from two or three—not all—options  

Daniel Hsu and his student Arushi Gupta show it is possible to build discrete choice models by estimating parameters from a small subset of options rather than having to analyze all possible options that may easily number in the thousands, or more. Using linear equations to estimate parameters in Hidden Markov chain choice models, the researchers were surprised to find they could estimate parameters from as few as two or three options. The results, theoretical for now, mean that in a world of choices, retailers and others can offer a small, meaningful set of well-selected items from which consumers are likely to find an acceptable choice even if their first choice is not available. For researchers, it means another tool to better model real-world behavior in ways not possible before.

Given several choices, what option will people choose? From the 1960s this simple question—of interest to urban planners, social scientists, and naturally, retailers—has been studied by economists and statisticians using discrete choice models, which statistically model the probabilities people will choose an option among a set of alternatives. (While an individual’s choice can’t be predicted, it is possible to study groups of people and infer patterns of behavior from sales, survey, and other data.)

In recent years, a type of discrete choice model called multinomial logit models has been commonly used. These models, easy to fit and understand, work by associating regression coefficients to each option based on behavior observed from real-world data. If ridership data shows people choose the subway 50% of the time and the bus 50% of the time, the model’s coefficients are tweaked to assign equal probability to each option.

On the whole, multinomial logit models perform well but fail to easily accommodate the introduction of new options that substitute for existing ones. If a second bus line is added and is similar to the existing one—same route, same frequency, same cost—except that the new bus line has articulated buses, a multinomial logit model would consider all three alternatives independently, splitting the proportion equally and assigning a probability of 0.33 to all three options.

“But that is not what happens,” says Daniel Hsu, a computer science professor and a member of the Data Science Institute who explores new algorithmic approaches to statistical problems. “People don’t care whether a bus is articulated or not. People just want to get to work.” Train riders especially don’t care about a new bus option because a bus is not a substitute for a train, and for this reason, the coefficient for trainer riders should not change.

The bus-train example is small, limited to three choices. In the real world, especially in retailing, choices are so numerous as to be overwhelming. People can’t be shown all options so retailers and others must offer a small set of choices from which people will find a substitute choice they are happy with even if their most preferred choice is not included.

To better model substitution behavior, researchers in Columbia’s Industrial Engineering and Operations Research (IEOR) Department—Jose Blanchet (now at Stanford University), Guillermo Gallego, and Vineet Goyal—two years ago proposed the use of Markov Chain models, which make predictions based on previous behaviors, or states. All options have probabilities as before, but the probability changes based on preceding options. What fraction of people will choose A when the previous states are B and C, or are C and D?  Removing one option, the most preferred one for example, changes the chain of probabilities, providing way for decide the next most preferred option among those remaining.

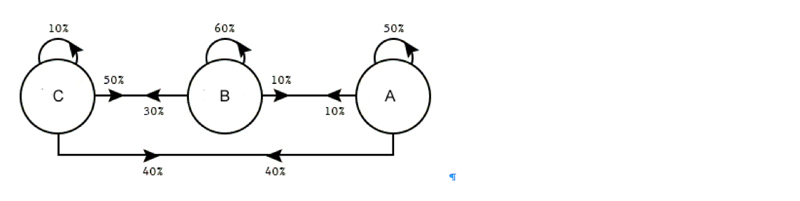
Switching from multinomial logit models to Markov chain choice models better captured substitution behavior but at the expense of much more complexity; previously, n possible options meant n parameters, but in the Markov chain models, n parameters just describes the initial probabilities; each removal of an option requires recalculating all possible combinations for a total of n squared parameters. Instead of 100 parameters, now it’s 10k parameters. Computers can handle this complexity; a consumer can’t and won’t.

The IEOR researchers showed it was possible to model substitution behavior by analyzing all possible options; left open was the possibility of doing so using less data, that is, some subset of the entire data set.

This was the starting point for Hsu and Arushi Gupta, a master’s student with an operations research background who had previously worked on estimating parameters for older discrete choice models; Gupta relished the opportunity to do the same for a more complex model.

“We looked at it as an algebraic puzzle,” says Hsu. “If you know two-thirds of people choose this option when these three are offered, how do you get there from the original Markov chain choice model? What are the parameters of the model that would give you this?”

Initially they set out to find an approximate solution but, changing tack, tried for the harder thing: getting a single exact solution. “Arushi discovered that all model parameters were related to the choice probabilities via linear equations, where the coefficients of the equations were given by yet other choice probabilities,” says Hsu.  “This is great because it means choice probabilities can be estimated from data. And this gives a way to potentially indirectly estimate all of the model parameters just by solving a system of equations.”

Says Gupta, “It is also quite lucky that it turned out to be just linear equations because even very big systems of linear equations are easy to solve on a computer. If the relationship had turned out to be other polynomial equations, then it would have been much more difficult.”

The final piece of the puzzle was to prove that the linear equations uniquely determined the parameters. “We crafted a new algebraic argument using the theory of a special class of matrices called M-matrices, which naturally arise in the study of Markov chains” says Hsu. “Our proof suggested that assortments as small as two and three item sets could yield linear equations that pin down the model parameters.”

Their results, detailed in Parameter identification in Markov chain choice models, showed a small amount of data suffices to pinpoint consumer choice behavior. The paper, which was presented at last year’s Conference on Algorithmic Learning Theory, is now published in the Proceedings of Machine Learning Research.

The researchers hope their results will lead to better ways of fitting choice models to data while helping understand the strengths and weaknesses of the models used to predict consumer choice behavior.

About the Researchers

Arushi Gupta, who received her bachelors at Columbia in 2016 in computer science and operations research, will earn a master’s degree in machine learning this May. In the fall, she starts her PhD in computer science at Princeton where she will study machine learning. In addition to Parameter identification in Markov chain choice models, she is coauthor of two additional papers, Do dark matter halos explain lensing peaks? and Non-Gaussian information from weak lensing data via deep learning.

Daniel Hsu is associate professor in the Computer Science Department and a member of the Data Science Institute, both at Columbia University, with research interests in algorithmic statistics, machine learning, and privacy. His work has produced the first computationally efficient algorithms for several statistical estimation tasks (including many involving latent variable models such as mixture models, hidden Markov models, and topic models), provided new algorithmic frameworks for solving interactive machine learning problems, and led to the creation of scalable tools for machine learning applications.

Before coming to Columbia in 2013,  Hsu he was a postdoc at Microsoft Research New England, and the Departments of Statistics at Rutgers University and the University of Pennsylvania. He holds a Ph.D. in Computer Science from UC San Diego, and a B.S. in Computer Science and Engineering from UC Berkeley. Hsu has been recognized with a Yahoo ACE Award (2014), selected as one of “AI’s 10 to Watch” in 2015 by IEEE Intelligent Systems, and received a 2016 Sloan Research Fellowship. Just last year, he was made a 2017 Kavli Fellow.

Posted 05/09/18
– Linda Crane