Indistinguishability obfuscation for secure software
Encrypting software so it performs a function without the code being intelligible was long thought by many to be impossible. But in 2013, researchers—unexpectedly and in a surprising way—demonstrated how to obfuscate software in a mathematically rigorous way using multilinear maps. This breakthrough, combined with almost equally heady progress in fully homomorphic encryption, is upending the field of cryptography and giving researchers for the first time an idea of what real, provable security looks like. The implications are immense, but two large problems remain: creating efficiency and providing a clear mathematical foundation. For these reasons, five researchers, including many of those responsible for the recent advances, have formed the Center for Encrypted Functionalities with funding provided by NSF. Allison Bishop Lewko is part of this center. In this interview she talks about the rapidly evolving security landscape, the center’s mandate, and her own role.
Question: What happened to make secure software suddenly seem possible?
Allison Bishop Lewko: The short answer is that in 2013, six researchers—Sanjam Garg, Craig Gentry, Shai Halevi, Mariana Raykova, Amit Sahai, Brent Waters—published a paper showing for the first time that it is possible to obfuscate software in a mathematically rigorous way using a new type of mathematical structure called multilinear maps (see sidebar for definition). This means I can take a software program and put it through the mathematical structure provided by these multilinear maps and encrypt software to the machine level while preserving its functionality. Anyone can take this obfuscated software and run it without a secret key and without being able to reverse-engineer the code. To see what’s happening in the code requires solving the hard problem of breaking these multilinear maps.
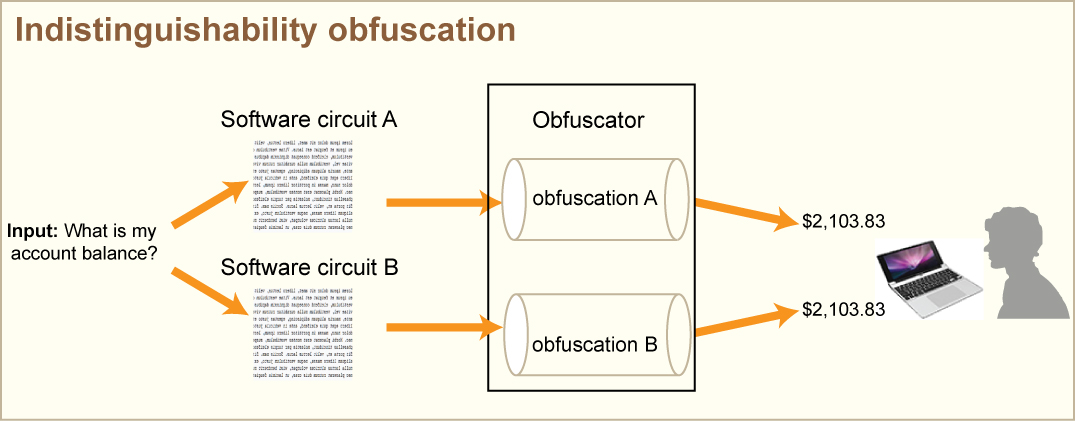
This process of encrypting software so it still executes, which we call indistinguishability obfuscation, was something we didn’t believe was out there even two or three years ago. Now there is this first plausible candidate indistinguishability obfuscator using multilinear maps.
And it’s rigorous. Today there are programs that purport to obfuscate software. They add dead code, change the variables, things you imagine you would get if you gave a sixth-grader the assignment to make your software still work but hard to read. It is very unprincipled and people can break it easily. Indistinguishability obfuscation is something else entirely.
Indistinguishability obfuscation is achieved when a software circuit is obfuscated in such a way that two different obfuscations are indistinguishable.
How does obfuscation differ from encryption?
Both obfuscation and encryption protect software, but the nature of the security guarantee is different. Encryption tells you your data or software is safe because it is unintelligible to anyone who doesn’t have the secret key to decrypt it. The software is protected but at a cost of not being usable. The software is either encrypted and protected, or it is decrypted and readable.
Obfuscation is a guarantee to protect software, but there is this added requirement that the encrypted software still has to work, that it still performs the function it was written to do. So I can give you code and you can run it without a secret key but you can’t learn how it works.
The bar is much higher for obfuscation because obfuscated software must remain a functional, executable program. Protecting software and using it at the same time is what is hard. It’s easy to protect software if you never have to use it again.
These concepts of encryption and decryption, however, do live very close together and they interact. Encryption is the tool used to accomplish obfuscation, and obfuscation can be used to build an encryption.
How so? Do you use the same methods to encrypt data to obfuscate code?
Not exactly, though the general concept of substituting something familiar with something seemingly random exists in both.
In the well-known RSA encryption method, each character of the output text is replaced by a number that gets multiplied by itself a number of times (the public key) to get a random-looking number that only the secret, private key can unlock and make sense of.
When you obfuscate software, each bit of the original program gets associated with some number of slots. For every slot there are two matrices, and every input bit determines what matrix to use.
Each bit is represented by one of two matrices, with 0 and 1 determining which matrix to use. The selected matrices are then multiplied together. Multiplying two matrices not meant to be multiplied prevents the software from being correctly reassembled.
The result is a huge chain of matrices. To compute the program on an input bit stream requires selecting the corresponding matrices and multiplying them.
Is having two matrices for every slot a way to add randomness?
No. The choice of what matrix to use is deterministic based on the input. But we do add randomness, which is a very important part of any cryptography scheme since it’s randomness that makes it hard to make out what’s going on. For this current candidate obfuscation scheme, we add randomness to the matrices themselves (by multiplying them by random matrices), and to representations we create of the matrices—like these multilinear maps.
But we do it very carefully. Among all these matrices, there are lots of relationships that have to be maintained. Adding randomness has to be done in a precise way so it’s enough to hide things but not so much to change software behavior.
There is this tension. The more functionality to preserve, the more there is to hide, and the harder it is to balance this tension. It’s not an obvious thing to figure out and it’s one reason why this concept of obfuscation didn’t exist until recently.
Amit Sahai, director of the Center, compares obfuscated software to a jigsaw puzzle, where the puzzle pieces have to fit together the right way before it’s possible to learn anything about the software. The puzzle pieces are the matrix encoded in the multilinear map, and the added randomness makes it that much harder to understand how these pieces fit together.
What does obfuscated software look like?
You would not want to see that. A small line becomes a page of random characters. The original code becomes bit by bit multiplication matrices. And this is one source of inefficiency.
Actually for this first candidate it’s not the original software itself being put through the obfuscation, but the software transformed into a circuit (a bunch of AND, OR, NOT gates), and this is another source of inefficiency.
Indistinguishability obfuscation is said to provide a richer structure for cryptographic methods. What does that mean?
All cryptography rests on trying to build up structures where certain things are fast to compute, and certain things are hard. The more you can build a richer structure of things that are fast, the more applications there are that can take advantage of this encryption. What is needed is a huge mathematical structure with a rich variety of data problems, where some are easy, some are hard.
In RSA the hard problem is factoring large numbers. One way—multiplying two prime numbers—is easy; that’s the encryption. Going back—undoing the factorization—is hard unless you have the key. But it’s hard in the sense that no one has yet figured out how to factorize large numbers quickly. That nobody knows how to factor numbers isn’t proven. We’re always vulnerable to having someone come out of nowhere with a new method.
RSA is what we’ve had since the 80s. It works reasonably well, assuming no one builds a quantum computer.
RSA is a single function where going one way is easy and one way is hard. It requires generating both a private and public key at the same time.
But RSA and other similar public key encryption schemes don’t work for more complicated policies where you want some people to see some data and some other people to see other data. RSA has one hard problem and allows for one key that reads everything. There’s no nuance. If you know the factors, you know the factors and you can read everything.
A dozen years ago (in 2001) Dan Boneh working with other people discovered how to build crypto systems using bilinear maps on elliptic curves (where the set of elements used to satisfy an equation consists of points on a curve rather than integers). Elliptic curves give you a little more structure than a single function; some things are easy to compute but there are things that are hard to compute. The same hard problem has different levels of structure.
Think of a group having exponents. Instead of telling you the process for getting an exponent out, I can give you one exponent, which to some extent represents partial information, and each piece of partial information lets you do one thing but not another. The same hard problem can be used to generate encryption keys with different levels of functionality, and it all exist within the same system.
This is the beginning of identity-based security where you give different people particular levels of access to encrypted data. Maybe my hospital sees a great deal of my data, but my insurance company sees only the procedures that were done.
Richer structures for hard problems expand the applications for cryptography.
The structure of bilinear maps allows for more kinds of keys with more levels of functionality than you would get with a simple one-way function. It’s not much of a stretch to intuitively understand that more is possible with trilinear maps or with multilinear maps.
For a dozen years it was an open problem on how to extend bilinear maps to multilinear maps in the realm of algebraic geometry, but elliptic curves didn’t seem to have a more computationally efficient structure on which to build. During this time, Craig Gentry (now at IBM) was working on fully homomorphic encryption, which allows someone to perform computations on encrypted data (the results will also be encrypted). Gentry was using lattices, a type of mathematical structure from number theory, an entirely different mathematical world than algebraic geometry.
Lattices provide a rich family of structures, and lattice schemes hide things by adding noise. As operations go on, noise gradually builds up and that’s what makes homomorphic encryption hard.
In lattice-based cryptography, encrypted data can be envisioned as points at some random distance from a point on a lattice (shown here in two dimensions, though lattices can have hundreds). On decryption, each blue point is attracted to the nearest lattice point. Homomorphic operations amplify the random displacements. If the noise exceeds a threshold, some points gravitate to the wrong lattice point, leading to the wrong decryption.
You might think immediately that these lattices schemes serve as a multilinear map but there isn’t a sharp divide between what’s easy and hard; there is a falloff. With fully homomorphic encryption having this gradual quality, it wasn’t at all clear how to use it in a way to build something where multiplying three things is easy but multiplying four things is hard.
The solution came in 2013 with the publication of Candidate Multilinear Maps from Ideal Lattices where the authors were able to make a sharp threshold between easy and hard problems within lattice problems. They did it by taking something like a fully homomorphic scheme and giving out a partial secret key; one that lets you do this one thing at level 10 but not at level 11. These partial keys, which are really weak secret keys, add more nuance, but it’s extremely tricky. If you give out a weak key, you may make things easy that you don’t want to be easy. You want it to break a little but not too badly. This is another source of inefficiency.
How soon before obfuscated software becomes a reality?
A long time. Right now, indistinguishability obfuscation is a proof of concept. Before it can have practical application, it should have two features: it should be fast, and we should have a good understanding of why it is secure, more than this-uses-math-and-it-looks-like-we-don’t-know-how-to-break-it.
Indistinguishability obfuscation currently doesn’t meet either criteria. It is extremely inefficient to what you want to run in real life—running an instance of a very simple obfuscated function would take seconds or minutes instead of microseconds—and we don’t have a good answer for why we believe it’s hard to break.
Is that the purpose of the Center for Encryption Functionalities?
Yes. The center’s main thrusts will be to increase efficiency and provide a provable mathematical foundation. Many of the same people responsible for the big advances in indistinguishability obfuscation and fully homomorphic encryption are working at the center and building on previous work.
We’ll be examining every aspect of the current recipe to increase efficiency. There are many avenues to explore. Maybe there is a more efficient way of implementing multilinear maps that doesn’t involve matrices. Maybe only certain parts of a program have to be encrypted. We’re still early in the process.
The center also has a social agenda, to both educate others on the rapid developments in cryptography and bring together those working on the problem.
What is your role?
My role is to really narrow down our understanding of what we’re assuming when we say indistinguishability obfuscation is secure. If someone today breaks RSA, we know they’ve factored big numbers, but what would it take to break indistinguishability obfuscation?
Indistinguishability obfuscation is still this very complicated, amorphous thing of a system with all these different possible avenues of attack. It’s difficult to comprehensively study the candidate scheme in its current form and understand exactly when we are vulnerable and when we are not.
I did my PhD in topics to expand the set of things that we can provably reduce to nice computational assumptions, which is very much what is at the heart of where this new obfuscation stuff is going. We need to take this huge, complicated scheme down to a simple computational problem to make it easy for people to study. Saying “factor two numbers” is a lot easier than saying break this process that takes a circuit to another circuit. We have to have this tantalizing carrot of a challenge to gain interest.
And on this front we have made great progress. We have a somewhat long, highly technical proof that takes an abstract obfuscation for all circuits and reduces it to a sufficiently simple problem that others can study and try to break.
That’s the first piece. What we don’t yet have is the second piece, which is instantiating the simple problem as a hard problem in multilinear maps.
Have there been any attempts to “break” indistinguishability obfuscation?
Yes, in the past few months some attacks did beat back on some problems contained in our proof that we thought might be hard, but these attacks did not translate into breaks on the candidate obfuscation scheme. While we wished the problems had been hard, the attacks help us narrow and refine the class of problems we should be focusing on, and they are a reminder that this line between what is hard and what is not hard is very much still in flux.
The attackers didn’t just break our problem, they broke a landscape of problems for current multilinear map candidates, making them fragile to use.
Were you surprised that the problem was broken?
Yes, very surprised, though not super-surprised because this whole thing is very new. There are always breaks you can’t imagine.
Do the breaks shake your faith in indistinguishability obfuscation?
I have no faith to be shaken. I simply want to know the answer.
We learn something from this process either way. If the current multilinear map candidates turn out to be irretrievably broken—and we don’t know that they are—we still learn something amazing. We learn about these mathematical structures. We learn about the structure of lattice-based cryptography, and the landscape of easy and hard problems.
Every time something is broken, it means someone came up with an algorithm for something that we didn’t previously know. Bilinear maps were first used to break things; then Dan Boneh said if it’s a fast algorithm that can break things, let’s re-appropriate it and use it to encrypt things. Every new algorithm is a potential new tool.
The fact that a particular candidate can be broken doesn’t make it implausible that other good candidates exist. We’ve also made progress on working with different kinds of computational models. In June, we will present Indistinguishability Obfuscation for Turing Machines with Unbounded Memory at STOC, which replaces circuits with a Turing machine to show conceptually that we can do obfuscation for varying input sizes.
Things are still new; what we’ve done this year at the center is motivating work in this field. People will be trying to build the best multilinear maps for the next 20 years regardless of what happens with these particular candidates.
The ongoing cryptanalysis is an important feedback loop that points to targets that attackers will go after to try to break the scheme, and it will help drive the direction of cryptography. It’s really an exciting time to be a researcher in this field.
About Allison Bishop Lewko
Allison Bishop Lewko is assistant professor of computer science at Columbia Engineering and a faculty affiliate of Columbia’s Institute for Data Science Institute and the Institute’s Cybersecurity Center. Her current areas of research are cryptography, complexity theory, harmonic analysis, combinatorics, and distributed computing.
Prior to joining Columbia, she was a postdoctoral researcher at Microsoft Research New England where she designed error-tolerant algorithms.
In 2013, she was named to the Forbes Under 30 for designing encryption algorithms.
Lewko received her PhD in Computer Science from UT-Austin where she was advised by Brent Waters. She has a certificate of advanced study in mathematics from the University of Cambridge and a bachelor’s degree in mathematics from Princeton University.
What is a multilinear map?
A multilinear map is a new type of mathematical structure from the field of number theory that has applications in cryptographic systems.
A multilinear map is a “mapping” among different groups in which an object from one group is multiplied by (or otherwise interacts with) an object in another group to create a new and different object. (The relatedness comes from both objects being possible solutions to the same hard mathematical problem.)
This mapping process makes it possible to disguise the original objects by using the new object when performing a function and still achieve the same overall data transformation that would have been produced without performing the mapping.
The mathematics behind multilinear maps is sophisticated and challenging to understand. In concept multilinear maps resemble bilinear maps—used in cryptographic systems for the past dozen years—where there is the notion of a bilinear mapping between the group of points on an elliptic curve and a finite field.
But where bilinear maps exist in the realm of algebraic geometry and use the discrete logarithm problem for points on a curve (computing quadratic functions in the exponent), multilinear maps originate in number theory. The recent constructions for cryptographic multilinear maps (proposed by Shai Halevi, Craig Gentry, Shai Halevi, Mariana Raykova, Amit Sahai, Brent Waters) use hard problems from ideal lattices where points are arranged on a high-dimensional lattice (similar to how they are used in fully homomorphic encryption schemes).
Lattices give rise to an abundance of potentially computationally difficult problems, providing a richer structure on which to build cryptographic systems and a finer level of control over what operations are easy and which are hard.
The rapid evolution of indistinguishability obfuscation—by papers
The current indistinguishability obfuscation scheme builds on a series of developments described in these papers, each of which generated its own stream of papers.
2009
Proposal for fully homomorphic encryption grounded in the known math around regular lattices: A Fully Homomorphic Encryption Scheme, PhD thesis by Craig Gentry (now at IBM).
Proposal for fully homomorphic encryption grounded in the known math around regular lattices: A Fully Homomorphic Encryption Scheme, PhD thesis by Craig Gentry (now at IBM).
March 2013
Multilinear maps from ideal lattices to supply hard problems for cryptography: Candidate Multilinear Maps from Ideal Lattices by Sanjam Garg, Craig Gentry, Shai Halevi. This paper in particular proposed a new mathematical building block, generating an explosion of papers. Most of exciting was which was:
Multilinear maps from ideal lattices to supply hard problems for cryptography: Candidate Multilinear Maps from Ideal Lattices by Sanjam Garg, Craig Gentry, Shai Halevi. This paper in particular proposed a new mathematical building block, generating an explosion of papers. Most of exciting was which was:
July 2013
Candidate Indistinguishability Obfuscation and Functional Encryption for all circuits by Sanjam Garg, Craig Gentry, Shai Halevi, Mariana Raykova, Amit Sahai, Brent Waters.
Candidate Indistinguishability Obfuscation and Functional Encryption for all circuits by Sanjam Garg, Craig Gentry, Shai Halevi, Mariana Raykova, Amit Sahai, Brent Waters.
Once this paper appeared and demonstrated how indistinguishability obfuscation can be achieved, other papers on obfuscation followed, with 50 appearing within six to eight months.
Applications for secure software
Any software that contains sensitive information becomes a potential application.
Hiding secrets inside software.
If software can be made unintelligible, other information like passwords, digital signature, and encryption keys can be hidden inside software. Two possibilities are immediately obvious. Anything can be a password, including an email. And passwords would not have to be exchanged ahead of time before sending the message.
If software can be made unintelligible, other information like passwords, digital signature, and encryption keys can be hidden inside software. Two possibilities are immediately obvious. Anything can be a password, including an email. And passwords would not have to be exchanged ahead of time before sending the message.
Protecting software patches. Security updates, or patches, intended to plug security holes may serve as a convenient pointer to the vulnerability being fixed, which hackers can then exploit in devices not yet updated.
Entrusting software to the cloud, or otherwise distributing proprietary or valuable algorithms. Valuable, sensitive, or proprietary software, once obfuscated, can be distributed without fear it will be reverse-engineered. Financial institutes can distribute trading algorithms. Software on captured military drones will remain unreadable. Manufacturers could distribute encrypted DVDs.
About The Center for Encrypted Functionalities (CEF)
The Center’s primary mission is to transform program obfuscation from an art to a rigorous mathematical discipline. It supports direct research, organizes retreats and workshops to bring together researchers, and engages in outreach and educational efforts.
Supported through an NSF Secure and Trustworthy Cyberspace Frontier Award, the Center has five principal investigators, including Amit Sahai (UCLA), who is director, Dan Boneh (Stanford), Susan Hohenberger (Johns Hopkins), Allison Bishop Lewko (Columbia), and Brent Waters (University of Texas, Austin).
Add to GMail