


Next: Affine Invariant
Up: Multiview Constraints for Recognition
Previous: Theorem 1:
If the image to image homography is affine, the transformation matrix
has
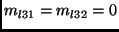 and
and 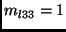 .
The transformation can be expressed in terms of inhomogeneous coordinates as
.
The transformation can be expressed in terms of inhomogeneous coordinates as
![\begin{displaymath}
{\bf x}^l[i] = {\bf A}_l{\bf x}^0[i] + {\bf b}_l
\end{displaymath}](img48.png) |
(3) |
where ![${\bf x}^l[i]$](img49.png) is the inhomogeneous representation of the
is the inhomogeneous representation of the 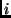 th point on the contour
in view
th point on the contour
in view 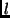 ,
, 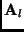 is the upper
is the upper 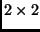 minor of
minor of 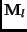 and
and 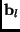 is the
upper two elements of the last column of
is the
upper two elements of the last column of 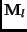 .
.
The above expression is valid for the scenarios when correspondence
between points across views is known. However in practice,
correspondence is rarely available. In case correspondence information
is not available, Equation 3 assumes the
form
where shifting 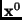 by
by 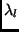 would align the corresponding
points of
would align the corresponding
points of 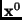 and
and 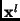 . The frequency domain
representation can be given by
. The frequency domain
representation can be given by
![\begin{displaymath}
{\bf X}^l[k] = {\bf A}_l{\bf X}^0[k] \exp({\frac{j 2 \pi \lambda_l k}{N}}),\;\;
0 < k < N
\end{displaymath}](img58.png) |
(4) |
if the 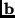 term is eliminated by omitting the
term is eliminated by omitting the 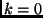 term in the
Fourier domain.
term in the
Fourier domain.
Subsections



Next: Affine Invariant
Up: Multiview Constraints for Recognition
Previous: Theorem 1:
2002-10-10