


Next: Constraints based on Phases
Up: Rank Constraints for Recognition
Previous: Rank Constraints for Recognition
The study of invariants has been pursued actively for many years. Invariants provide us
with the ability to come up with representations of the features in a scene that do not depend on the view, and can prove
to be extremely handy for purposes of recognising objects from multiple views.
In this Subsection we explore the possibility of deriving an affine invariant for a contour.
Let us define a measure called the cross-conjugate
product (CCP) on the Fourier representations of two views
as
The matrix 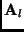 can be expressed as a sum
of a symmetric matrix and a skew symmetric matrix as
can be expressed as a sum
of a symmetric matrix and a skew symmetric matrix as
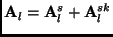 where
where
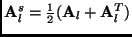 and
and
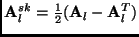 . The skew symmetric matrix
reduces to
. The skew symmetric matrix
reduces to
where
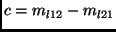 is the difference of the
off-diagonal elements of
is the difference of the
off-diagonal elements of 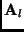 . We now have
. We now have
The first term of the
above equation is purely real and the second term is purely
imaginary.
We observe that the effect of the transformation matrix 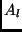 on the second term is restricted to a scaling by a factor
on the second term is restricted to a scaling by a factor 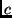 . We
can define a new measure
. We
can define a new measure 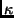 , ignoring scale, for the
sequence
, ignoring scale, for the
sequence
 in view
in view 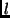 as
as
![\begin{displaymath}
\kappa(l)[k] = {\bf\bar{X}}^l[k]^{*T} \left[ \begin{array}{cr} 0 & 1 \\
-1\;\; & 0 \end{array} \right] {\bf\bar{X}}^l[k].
\end{displaymath}](img74.png) |
(6) |
It can be shown [7] that
![\begin{displaymath}
\kappa (l)[k] = \vert{\bf A}_l\vert\; \kappa(0)[k] ,\;\;\; 0 < k < N
\end{displaymath}](img75.png) |
(7) |
Equation 7 gives a necessary condition for the
sequences
 and
and
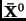 to be two
different views of the same planar shape, or in other words, the
values of the measure
to be two
different views of the same planar shape, or in other words, the
values of the measure 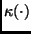 in the two views
should be scaled versions of each other. This extends to
multiple views also. Consider the
in the two views
should be scaled versions of each other. This extends to
multiple views also. Consider the
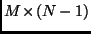 matrix formed by the coefficients
of the
matrix formed by the coefficients
of the 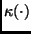 measures for M different views.
measures for M different views.
The necessary condition for matching of the planar shape
in 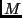 views then reduces to
views then reduces to
 |
(8) |
It should be noted that this recognition constraint does not
require correspondence between views and is valid for any
number of views.
Since, the 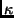 measures in the various views are only scaled versions of
each other, if we normalize the
measures in the various views are only scaled versions of
each other, if we normalize the 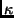 measure terms in each view with respect to
a fixed one then
measure terms in each view with respect to
a fixed one then
These terms of the normalized 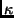 measure - the
measure - the 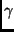 measure are independent of the view.
Hence,
measure are independent of the view.
Hence, 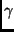 is an affine view invariant of a contour, whose computation does not
need correspondence information across views.
is an affine view invariant of a contour, whose computation does not
need correspondence information across views.



Next: Constraints based on Phases
Up: Rank Constraints for Recognition
Previous: Rank Constraints for Recognition
2002-10-10
![$\displaystyle ({\bf\bar{X}}^0[k])^{*T} {\bf A}_l {\bf\bar{X}}^0[k] \exp({\frac{j 2 \pi \lambda_l k}{N} }).$](img64.png)
![\begin{displaymath}\Theta =
\left[ \begin{array}{ccc}
\kappa(0)[1] & \cdots & \...
...kappa(M-1)[1] & \cdots & \kappa(M-1)[N-1]
\end{array} \right]
\end{displaymath}](img79.png)
![]() measures in the various views are only scaled versions of
each other, if we normalize the
measures in the various views are only scaled versions of
each other, if we normalize the ![]() measure terms in each view with respect to
a fixed one then
measure terms in each view with respect to
a fixed one then