


Next: Results and Discussions
Up: Rank Constraints for Recognition
Previous: Constraints based on Phases
Unless properly taken care, the phase based algebraic constraints can
have problems with the phase wrap around. We now present a rank-three
constraint based on magnitudes of the vector Fourier coefficients.
We start with Equation 4. This equation can be rewritten as
Writing in terms of the real and imaginary components of the complex numbers
Taking the square of the magnitudes of both sides, we get
Similarly,
Its evident from equations 14 and 15
that the magnitude of the components of the Fourier domain representation
in any view can be expressed in terms of the components in a reference
view.
This result can also be expressed in the following manner. Given 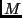 views, we can construct a (
views, we can construct a (
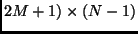 matrix as follows. The first
row consists of the sum of products
matrix as follows. The first
row consists of the sum of products
![$( U^0_R[k] V^0_R[k] + U^0_I[k]
V^0_I[k])$](img140.png) ,
, 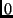 being the reference view. Every view contributes two rows
to this matrix (except the reference view, which contributes 3 rows) the
magnitudes of
being the reference view. Every view contributes two rows
to this matrix (except the reference view, which contributes 3 rows) the
magnitudes of 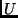 in one row and the magnitudes of
in one row and the magnitudes of 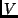 in the other. Let
in the other. Let
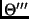 =
=
![\begin{displaymath}
{\tiny \left [ \begin{array}{ccc}
(U^0_R[1] V^0_R[1] + U^0_...
...... & ((V^M_R[G])^2 + (V^M_I[G]) ^ 2)
\end{array} \right ]
}
\end{displaymath}](img143.png) |
(16) |
(using 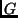 for
for 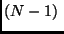 )
)
From equations 14 and 15, one can
conclude that the rank of 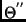 is 3, irrespective of the number
of views. Therefore, the constraint,
is 3, irrespective of the number
of views. Therefore, the constraint,
 |
(17) |
is a necessary condition for recognition in multiple views related by
affine image-to-image homographies. This observation is consistent with
the notion that the various views of a shape lie in a lower dimensional
linear subspace. We can also say that the squares of the magnitudes of
the Fourier Domain representation of a contour can be used as a signature
of the boundary. These are, naturally, view independent as they can be
computed from a single view.
Figure 1:
Four affine transformed views of a dinosaur
(a) 
|
(b) 
|
(c) 
|
|



Next: Results and Discussions
Up: Rank Constraints for Recognition
Previous: Constraints based on Phases
2002-10-10
![$\displaystyle U^l[k] = (m_{l11} U^0[k] + m_{l12} V^0[k]) \exp({\frac{j2\pi\lambda_l k}{N}})$](img118.png)
![$\displaystyle V^l[k] = (m_{l21} U^0[k] + m_{l22} V^0[k]) \exp({\frac{j2\pi\lambda_l k}{N}})$](img119.png)
![$\displaystyle U^l[k] = (m_{l11} U^0[k] + m_{l12} V^0[k]) \exp({\frac{j2\pi\lambda_l k}{N}})$](img118.png)
![$\displaystyle V^l[k] = (m_{l21} U^0[k] + m_{l22} V^0[k]) \exp({\frac{j2\pi\lambda_l k}{N}})$](img119.png)
![]() views, we can construct a (
views, we can construct a (
![]() matrix as follows. The first
row consists of the sum of products
matrix as follows. The first
row consists of the sum of products
![]() ,
, ![]() being the reference view. Every view contributes two rows
to this matrix (except the reference view, which contributes 3 rows) the
magnitudes of
being the reference view. Every view contributes two rows
to this matrix (except the reference view, which contributes 3 rows) the
magnitudes of ![]() in one row and the magnitudes of
in one row and the magnitudes of ![]() in the other. Let
in the other. Let
![]() =
=
![\begin{displaymath}
{\tiny \left [ \begin{array}{ccc}
(U^0_R[1] V^0_R[1] + U^0_...
...... & ((V^M_R[G])^2 + (V^M_I[G]) ^ 2)
\end{array} \right ]
}
\end{displaymath}](img143.png)
![]() is 3, irrespective of the number
of views. Therefore, the constraint,
is 3, irrespective of the number
of views. Therefore, the constraint,