


Next: Rank Constraints for Recognition
Up: Problem Formulation
Previous: Problem Formulation
The Fourier transform and the collineation commute
with the above representation. That is, if points are transformed between
views 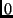 and
and 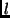 using Equation 1, the same homography will
transform corresponding frequency terms in the Fourier domain also. In other
words,
using Equation 1, the same homography will
transform corresponding frequency terms in the Fourier domain also. In other
words,
![\begin{displaymath}
{\bf X}^l[k] = {\bf M}_l{\bf X}^0[k] \mbox{ , } 0 \le k < N.
\end{displaymath}](img34.png) |
(2) |
Proof: Let
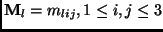 .
Expanding Equation 1 for the
.
Expanding Equation 1 for the 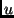 term,
term,
Taking the Fourier transform of the above equation and using the linearity
property of Fourier transforms, we get
Similarly for ![$V^l[k]$](img39.png) and
and ![$W^l[k]$](img40.png) . It is now easy to see that
. It is now easy to see that
giving us the desired result. 
Given a set of 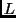 views, the recognition problem can be formulated as
the identification of a view-independent function
views, the recognition problem can be formulated as
the identification of a view-independent function 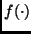 such that
such that
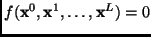 . This recognition
constraint can be linear or nonlinear in image coordinates. The algebraic
relation given by
. This recognition
constraint can be linear or nonlinear in image coordinates. The algebraic
relation given by 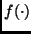 can then be used to settle the question
whether the
can then be used to settle the question
whether the 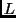 observed views were of the same object.
observed views were of the same object.



Next: Rank Constraints for Recognition
Up: Problem Formulation
Previous: Problem Formulation
2002-10-10
![]() views, the recognition problem can be formulated as
the identification of a view-independent function
views, the recognition problem can be formulated as
the identification of a view-independent function ![]() such that
such that
![]() . This recognition
constraint can be linear or nonlinear in image coordinates. The algebraic
relation given by
. This recognition
constraint can be linear or nonlinear in image coordinates. The algebraic
relation given by ![]() can then be used to settle the question
whether the
can then be used to settle the question
whether the ![]() observed views were of the same object.
observed views were of the same object.