


Next: Constraints based on Magnitudes
Up: Rank Constraints for Recognition
Previous: Affine Invariant
If 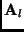 is a symmetric matrix (in Equation 5), it can be shown that the
auto-correlation
is a symmetric matrix (in Equation 5), it can be shown that the
auto-correlation 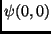 is real. This implies that
that the phase of
is real. This implies that
that the phase of 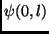 would be
would be
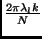 .
.
If we have 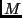 views, then we can form a
views, then we can form a
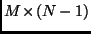 matrix
matrix
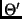 with the phase angles of
with the phase angles of
![$\psi(0,l)[k], 0 < k < N$](img92.png) forming the
row
forming the
row 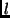 . It is clear that the rows of the matrix differ only by a scale
factor. Therefore,
. It is clear that the rows of the matrix differ only by a scale
factor. Therefore,
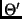 is a rank deficient matrix with a fixed rank
of 1, irrespective of the number of views. Therefore a necessary
condition for recognition in multiple views related by symmetric affine
homographies is
is a rank deficient matrix with a fixed rank
of 1, irrespective of the number of views. Therefore a necessary
condition for recognition in multiple views related by symmetric affine
homographies is
 |
(10) |
This rank-one constraint implies that the phases of CCP in different
views are linearly related. Thus, the phases form a signature of the
shape that is invariant to affine transformations. Unfortunately this
relationship is valid only if the affine transformation (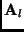 ) is
symmetric. Also, the CCP is computed between each view and a fixed
reference view; it thus depends on two views.
) is
symmetric. Also, the CCP is computed between each view and a fixed
reference view; it thus depends on two views.
For affine transformations when 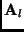 can be arbitrary, we derive
a rank-two constraint as follows.
can be arbitrary, we derive
a rank-two constraint as follows. 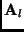 now contains a
skew-symmetric component in addition to a symmetric one. We define a new
measure
now contains a
skew-symmetric component in addition to a symmetric one. We define a new
measure
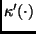 , which correlates each Vector Fourier
coefficient with a fixed one within each view.
, which correlates each Vector Fourier
coefficient with a fixed one within each view.
for any fixed 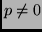 .
Equation 11 states that the phases of
.
Equation 11 states that the phases of 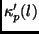 and
and
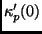 differ by an amount proportional to the shift
differ by an amount proportional to the shift 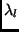 and the differential frequency
and the differential frequency 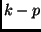 . Therefore, the ratio
. Therefore, the ratio
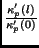 will be a complex sinusoid
will be a complex sinusoid
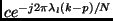 . The value of
. The value of 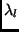 can be computed
from the inverse Fourier transform of the quotient series. Thus, the
phases of
can be computed
from the inverse Fourier transform of the quotient series. Thus, the
phases of 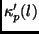 can be used as a signature for the contour.
can be used as a signature for the contour.
We can also form a 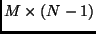 matrix
matrix
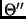 , similar to
the one above, that stacks the phases of
, similar to
the one above, that stacks the phases of
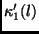 (taking
(taking
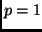 ). It will have the form
). It will have the form
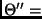
![\begin{displaymath}
{\scriptsize \left[ \begin{array}{ccccc}
\theta_1 & \theta_2...
... \ldots & \theta_{N-1} + (N-2)\phi_{M-1}
\end{array} \right]
}
\end{displaymath}](img111.png) |
(12) |
where 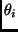 are the phases of
are the phases of 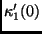 and
and
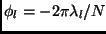 . This matrix will have a rank of 2 irrespective of
. This matrix will have a rank of 2 irrespective of
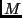 . The rank constraint on the above matrix, which is a necessary
condition for recognition of shapes in views related by affine
image-to-image homographies, is
. The rank constraint on the above matrix, which is a necessary
condition for recognition of shapes in views related by affine
image-to-image homographies, is
 |
(13) |
We see that 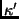 can be computed from a single view. Thus, the
phases of
can be computed from a single view. Thus, the
phases of 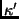 values provide a truly view-independent description
of the boundary.
values provide a truly view-independent description
of the boundary.
Experiments were conducted to affirm the validity of the above constraint.
Figure 1 shows four affine transform related views of a dinosaur.
When the
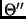 was constructed from the
was constructed from the
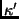 measures of the four views (a), (b), (c) and (d), with random shifts applied
to the boundary representations in each view, the rank of
measures of the four views (a), (b), (c) and (d), with random shifts applied
to the boundary representations in each view, the rank of
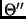 was
found to be essentially 2, the three greatest singular values being 33952.7, 58.8366, and 0.00242446.
was
found to be essentially 2, the three greatest singular values being 33952.7, 58.8366, and 0.00242446.



Next: Constraints based on Magnitudes
Up: Rank Constraints for Recognition
Previous: Affine Invariant
2002-10-10
![]() views, then we can form a
views, then we can form a
![]() matrix
matrix
![]() with the phase angles of
with the phase angles of
![]() forming the
row
forming the
row ![]() . It is clear that the rows of the matrix differ only by a scale
factor. Therefore,
. It is clear that the rows of the matrix differ only by a scale
factor. Therefore,
![]() is a rank deficient matrix with a fixed rank
of 1, irrespective of the number of views. Therefore a necessary
condition for recognition in multiple views related by symmetric affine
homographies is
is a rank deficient matrix with a fixed rank
of 1, irrespective of the number of views. Therefore a necessary
condition for recognition in multiple views related by symmetric affine
homographies is
![]() can be arbitrary, we derive
a rank-two constraint as follows.
can be arbitrary, we derive
a rank-two constraint as follows. ![]() now contains a
skew-symmetric component in addition to a symmetric one. We define a new
measure
now contains a
skew-symmetric component in addition to a symmetric one. We define a new
measure
![]() , which correlates each Vector Fourier
coefficient with a fixed one within each view.
, which correlates each Vector Fourier
coefficient with a fixed one within each view.
![]() matrix
matrix
![]() , similar to
the one above, that stacks the phases of
, similar to
the one above, that stacks the phases of
![]() (taking
(taking
![]() ). It will have the form
). It will have the form
![]()
![\begin{displaymath}
{\scriptsize \left[ \begin{array}{ccccc}
\theta_1 & \theta_2...
... \ldots & \theta_{N-1} + (N-2)\phi_{M-1}
\end{array} \right]
}
\end{displaymath}](img111.png)
![]() was constructed from the
was constructed from the
![]() measures of the four views (a), (b), (c) and (d), with random shifts applied
to the boundary representations in each view, the rank of
measures of the four views (a), (b), (c) and (d), with random shifts applied
to the boundary representations in each view, the rank of
![]() was
found to be essentially 2, the three greatest singular values being 33952.7, 58.8366, and 0.00242446.
was
found to be essentially 2, the three greatest singular values being 33952.7, 58.8366, and 0.00242446.