Having processed an ensemble of training images with Karhunen-Loeve
decomposition and having witnessed its face-compression abilities,
we now turn our attention to its usefulness in signal detection. The KL
decomposition has mapped each individual face ![]() into a
60-dimensional key describing the linear combination of an orthonormal basis
with a residual error, residuex. We wish to have a scalar measure of how
face-like a new image vector is by comparing it to the collection of faces we
have already considered. Each face in our database maps to a point in KL-space and
these points form a roughly Gaussian cluster. A new image will also map into a
point in this space. By observing how close the point is to the cluster
formed by D, we can measure how ``face-like'' it is. Thus, we can detect faces
in a scene with this measure and reject non-face images.
into a
60-dimensional key describing the linear combination of an orthonormal basis
with a residual error, residuex. We wish to have a scalar measure of how
face-like a new image vector is by comparing it to the collection of faces we
have already considered. Each face in our database maps to a point in KL-space and
these points form a roughly Gaussian cluster. A new image will also map into a
point in this space. By observing how close the point is to the cluster
formed by D, we can measure how ``face-like'' it is. Thus, we can detect faces
in a scene with this measure and reject non-face images.
Before we proceed, we shall add a dimension to the 60-dimensional space we
have formed from our key. The value of residue indicates how well the KL
decomposition approximates our image with its eigenvectors. Thus, a human face
will be well approximated since the eigenvectors we formed from the database
are optimal for such a task. Consequently, human faces should yield low
residue values. A non-face will generate a high residue value since it is
not in the span of the eigenfaces and can not be expressed as a linear
combination of the face-like eigenvectors. As was the case for each value in
the 60-dimensional key, the value of residue is expected to have a Gaussian
distribution over the vectors in the dataset. The ![]() value of this
distribution is
value of this
distribution is
![]() .
.
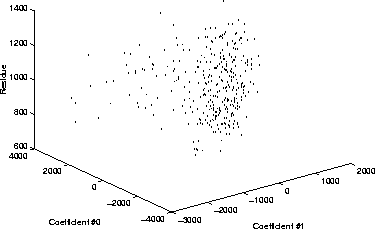
Figure ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) depicts the distribution of the first two coefficients
(c0,c1) of the key on the (x,y) plane and in the residue dimension on
the z-axis (or vertical). Note the multivariate distribution is now
61-dimensional with the addition of the residue dimension. A new image
vector that is presented to the KL-decomposition algorithm will map into a
point in this 61-dimensional cloud. The closer it is to the 61-dimensional
cloud of previously encountered points, the more face-like it appears. The
probability of membership within the class of faces is defined via a
probability density function (p.d.f or ``pdf'') similar to the one in
Equation
depicts the distribution of the first two coefficients
(c0,c1) of the key on the (x,y) plane and in the residue dimension on
the z-axis (or vertical). Note the multivariate distribution is now
61-dimensional with the addition of the residue dimension. A new image
vector that is presented to the KL-decomposition algorithm will map into a
point in this 61-dimensional cloud. The closer it is to the 61-dimensional
cloud of previously encountered points, the more face-like it appears. The
probability of membership within the class of faces is defined via a
probability density function (p.d.f or ``pdf'') similar to the one in
Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . We now discuss the pdf that will be used in our
``faceness'' equation.
. We now discuss the pdf that will be used in our
``faceness'' equation.
 |
The pdf we need must have a centroid at (0,0,0,...0) for all dimensions. Even
though the mean residue value (which is always positive) in the database is
not 0, we shall consider it to be 0. This is because the true centroid or mean
of the data-set is the mean face (which we computed in
Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) ). The locus of the mean face in the 61-dimensional
space is the 0-vector and so the centroid of the Gaussian distribution is the
0-vector (0,0,0...).
). The locus of the mean face in the 61-dimensional
space is the 0-vector and so the centroid of the Gaussian distribution is the
0-vector (0,0,0...).
Now, we analyse the 61-dimensional cloud of points we are trying to model. We wish to determine which Gaussian pdf will suit our needs. The value of this pdf will measure the ``faceness'' of an image by how close it is to this cloud of points determined by our original dataset, D.
We note, as expected [17], that the distribution of the points in
the cloud is a multi-variate Gaussian with a different ![]() value in each
of its 61 dimensions. However, an important observation is that the
distribution has its worst-case outliers at different extrema or distances
along each dimension. In other words, the worst-case or
value in each
of its 61 dimensions. However, an important observation is that the
distribution has its worst-case outliers at different extrema or distances
along each dimension. In other words, the worst-case or ![]() distance
along each dimension is not constant. Even more importantly, it is not
proportional to the
distance
along each dimension is not constant. Even more importantly, it is not
proportional to the ![]() value along the corresponding dimension.
value along the corresponding dimension.
Observe the data-distribution of c1,c2 and c3 in
Figure ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . The face points in the histograms seem to have a
Gaussian distribution in each dimension. Note the presence of extreme
outliers on either side of the plots. These are still valid faces despite
their location to the far left and the far right of the bell-curve. If we
approximate the distribution by a tightly-fitting Gaussian function, those
outliers will be given an extremely low likelihood value. However, they are
true faces and should therefore register a strong ``faceness'' probability.
Thus, an equation similar to Equation
. The face points in the histograms seem to have a
Gaussian distribution in each dimension. Note the presence of extreme
outliers on either side of the plots. These are still valid faces despite
their location to the far left and the far right of the bell-curve. If we
approximate the distribution by a tightly-fitting Gaussian function, those
outliers will be given an extremely low likelihood value. However, they are
true faces and should therefore register a strong ``faceness'' probability.
Thus, an equation similar to Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) will not suit us as a
face-detector since it will reject outliers.
will not suit us as a
face-detector since it will reject outliers.
Traditionally, statistically approaches to distribution modelling attempt to fit a Gaussian to the distribution in an L2 sense [17]. However, we choose to consider an envelope that wraps around the whole cloud of face-points (enclosing all outliers as well). The shape of this envelope is hyper-ellipsoidal. The envelope is not defined by the variance in the data set or by fitting to the points in the data set. Instead, it is shaped to contain all the points in the dataset and thus is defined by the boundary of the cloud or the most extreme points in the cloud. These are all valid faces and therefore a detector should not discard them, regardless of their distance to the cloud in an L2 sense.
Therefore, the sigmas in the Gaussian pdf that we use for detection should not
be related to the variance of the data in each dimension. Using the variance,
as we have shown, will cause misdetection of the odd outliers. However, these
outliers which lie quite far from the cluster are still valid faces.
Therefore, we shall select the ![]() values for our multivariate Gaussian
to be equal to the distance of the worst outlier in each dimension
(outlieri as given by Equation
values for our multivariate Gaussian
to be equal to the distance of the worst outlier in each dimension
(outlieri as given by Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) and
outlierresidue is
given by Equation
and
outlierresidue is
given by Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) ). The consequent pdf is computed using
Equation
). The consequent pdf is computed using
Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) :
:
Alternatively, we can write the faceness value as a distance from the cloud.
This distance is obtained by computing the logarithm of
Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . Thus, our distance from facespace measure
(DFFS) can be defined by Equation
. Thus, our distance from facespace measure
(DFFS) can be defined by Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) (note that k is an
arbitrary constant used to scale the output for display purposes):
(note that k is an
arbitrary constant used to scale the output for display purposes):
This DFFS measure is similar to Turk and Pentland's [44] approach to detection via a distance-to-facespace technique [44]. However, their technique merely utilizes the residue value in the computation and assumes all ck are 0. Consequently, this form of distance measure assumes that faces form a hyperplane in image-space. We can see that this is not the case since the cluster of face-points we have generated appears to form a hyper-ellipsoidal cloud shape. Additionally, in Turk and Pentland's technique, an image which happens to be spanned nicely by eigenfaces will be classified as a face. Unfortunately, eigenfaces, (especially higher-order ones) can be linearly combined to form images which do not resemble faces at all. Hence, merely using the residue as a faceness measure is not reasonable.
Figure ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) shows some sample faces and non-faces with their
corresponding ``DFFS'' value. The DFFS can be used for face-detection since it
yields low values for faces and high values for non-faces. The DFFS value is
not exactly zero for true faces since only the mean face is located precisely
in the center of the cloud representing the distribution. All other faces have
a distance from the center of the cloud and, consequently, have a non-zero
DFFS.
shows some sample faces and non-faces with their
corresponding ``DFFS'' value. The DFFS can be used for face-detection since it
yields low values for faces and high values for non-faces. The DFFS value is
not exactly zero for true faces since only the mean face is located precisely
in the center of the cloud representing the distribution. All other faces have
a distance from the center of the cloud and, consequently, have a non-zero
DFFS.
![\begin{figure}\center
\begin{tabular}[b]{ccccc}
\epsfig{file=norm/figs/dffs1....
...r} \\ \vspace*{0.5cm}
\epsfig{file=norm/figs/hand.ps,height=5cm}
\end{figure}](img235.gif) |