



Next: Using KL as a
Up: Karhunen-Loeve Decomposition for Statistical
Previous: Decoding a Key into
Note that the original vectors and the eigenvectors are all n-tuples with
n=7000. Therefore, the computation of the 60-dimensional key
(c0, c1,
..., c59) given by Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) requires convolution of
the input image (an arbitrary
requires convolution of
the input image (an arbitrary 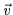 n-tuple) with 60 eigenvectors (the
n-tuple) with 60 eigenvectors (the
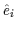 n-tuples). Thus, 60 convolutions of 7000 pixel masks must be
performed each time to convert an image into its key. To reduce this
computation, we have also generated scaled versions of the input vectors and
eigenvectors. These images are
n-tuples). Thus, 60 convolutions of 7000 pixel masks must be
performed each time to convert an image into its key. To reduce this
computation, we have also generated scaled versions of the input vectors and
eigenvectors. These images are
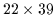 pixels and require n=858 element
vectors. However, the computation of
(c0, c1,..., c59) for the smaller
vectors requires roughly
pixels and require n=858 element
vectors. However, the computation of
(c0, c1,..., c59) for the smaller
vectors requires roughly  of the original processing time. The mean
face for the smaller data set is shown in Figure
of the original processing time. The mean
face for the smaller data set is shown in Figure ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . Thus, these
versions of the KL decomposition can be useful when time is more critical than
resolution or precision. However, the quality of such low resolution images
makes them unreliable for face recognition purposes. These should only be used
to perform coarse face detection. We shall now describe a technique for
detecting a face using an image's 60-scalar KL code.
. Thus, these
versions of the KL decomposition can be useful when time is more critical than
resolution or precision. However, the quality of such low resolution images
makes them unreliable for face recognition purposes. These should only be used
to perform coarse face detection. We shall now describe a technique for
detecting a face using an image's 60-scalar KL code.
Figure 4.28:
The mean face generated with smaller mug-shots.
 |




Next: Using KL as a
Up: Karhunen-Loeve Decomposition for Statistical
Previous: Decoding a Key into
Tony Jebara
2000-06-23

![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) requires convolution of
the input image (an arbitrary
requires convolution of
the input image (an arbitrary ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . Thus, these
versions of the KL decomposition can be useful when time is more critical than
resolution or precision. However, the quality of such low resolution images
makes them unreliable for face recognition purposes. These should only be used
to perform coarse face detection. We shall now describe a technique for
detecting a face using an image's 60-scalar KL code.
. Thus, these
versions of the KL decomposition can be useful when time is more critical than
resolution or precision. However, the quality of such low resolution images
makes them unreliable for face recognition purposes. These should only be used
to perform coarse face detection. We shall now describe a technique for
detecting a face using an image's 60-scalar KL code.