We now describe a strategy for selecting the shot that is most likely to succeed. Starting from the cue-ball, we compute linear trajectories to all solid balls (or striped balls if the user selects to play as stripes). We then compute linear trajectories from these to the detected pockets. Then we test each of these possible trajectories: from cue-ball to solid-ball to pocket to find those that don't involve any collisions with other objects. If no solid balls are found, we test the 8-ball for possible trajectories.
We then weight each of the 'valid' trajectories by the following
heuristics. Each time the user is to take a shot, we are really
interested in the angle at which he or she hits the cue ball (we shall
assume that the force with which the cue ball is hit is going to be
determined by the user). So, what is fundamentally being suggested to
the user is an angle at which to hit a cue ball, say 
as a
deviation from the line connecting the cue ball to the solid ball. The
more accuracy we need on , the harder the
shot. Figure 
shows how we can determine the
required angle. The distance from the cue-ball to the solid-ball is
l and the distance from there to the pocket is L. The angle formed
by the three objects is 
at the solid ball. We can compute
using this information as well as a bound on the maximum
error on which is 
.
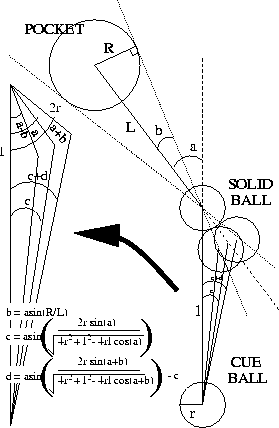
Figure: Determining the Angle and the Difficulty
For each possible shot, we compute 
and display to the user
the shot with the greatest value of (the shot which
requires the least accuracy) with the required trajectory (along
) superimposed on the image. This is a simplified
first-order strategy model since it is only 2D and does not include
spin effects, kinematics or rebounds in the computation of the shots.