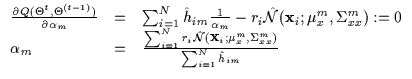 |
(7.19) |
The update for ![]() is a function of the
is a function of the ![]() and the
and the
![]() .
It is possible to keep this equality and use it later
as we derive the update rules for the means and the
covariances. However, it is quite cumbersome to manipulate
analytically if it is maintained as shown above. Thus, we lock the
values of
.
It is possible to keep this equality and use it later
as we derive the update rules for the means and the
covariances. However, it is quite cumbersome to manipulate
analytically if it is maintained as shown above. Thus, we lock the
values of ![]() and
and
![]() at their previous estimates
(i.e. at
at their previous estimates
(i.e. at
![]() )
and numerically update the
)
and numerically update the ![]() mixing
proportions.
mixing
proportions.
Since we are maximizing a bound, the above update rule increases conditional likelihood monotonically. This was also verified with a numerical implementation.