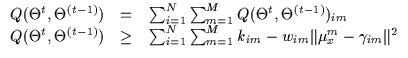 |
(7.21) |
Once again, the contact point for this parabola (i.e. the
![]() )
is the value for the previous model
)
is the value for the previous model
![]() or
the mean of the gate before any iteration. Let us denote the previous
parameters of the gate as
or
the mean of the gate before any iteration. Let us denote the previous
parameters of the gate as
![]() and
and
![]() .
To
facilitate the derivation, we can perform what is commonly called a
whitening operation on the coordinate system for each gate. For
each gate, we can consider that its previous parameters where
zero-mean and identity covariance. This is done by applying an affine
transformation to the
.
To
facilitate the derivation, we can perform what is commonly called a
whitening operation on the coordinate system for each gate. For
each gate, we can consider that its previous parameters where
zero-mean and identity covariance. This is done by applying an affine
transformation to the ![]() -space (i.e. shifting the data points
-space (i.e. shifting the data points
![]() appropriately). The data is translated by the mean and
scaled by the inverse of the square root of the covariance
matrix. In theory, nothing changes except that each gate observes
affinely displaced data instead and it then seems to have a zero mean
and identity covariance as its previous operating point. This
whitening operation does not need to be done explicitly
(i.e. numerically) but helps simplify the following derivation for the
bound.
appropriately). The data is translated by the mean and
scaled by the inverse of the square root of the covariance
matrix. In theory, nothing changes except that each gate observes
affinely displaced data instead and it then seems to have a zero mean
and identity covariance as its previous operating point. This
whitening operation does not need to be done explicitly
(i.e. numerically) but helps simplify the following derivation for the
bound.
Thus, without loss of generality, we consider that each data point has
been appropriately whitened for each gate. The result is that
![]() and
and
![]() .
Using
this assumption, we can compactly solve for the parameters of the
bounding parabola (
.
Using
this assumption, we can compactly solve for the parameters of the
bounding parabola (
![]() ). This is done by
meeting the three requirements (contact, tangentiality and
tightness). The results is shown in
Equation 7.23.
). This is done by
meeting the three requirements (contact, tangentiality and
tightness). The results is shown in
Equation 7.23.
As shown earlier, if a globally valid bound is desired, the value of
wim must always be greater than the expression in
Equation 7.23 no matter what the value of
![]() .
Thus we can find the minimum wim (i.e. wminim)
for which this is true and form a parabolic bound for the Q function
that is as 'tight' as possible. We shall now determine an efficient
way to compute wminim without searching the high dimensional
space of
.
Thus we can find the minimum wim (i.e. wminim)
for which this is true and form a parabolic bound for the Q function
that is as 'tight' as possible. We shall now determine an efficient
way to compute wminim without searching the high dimensional
space of ![]() each iteration.
each iteration.
Note in the expression for wim above that ![]() is used
only in an inner product with itself (
is used
only in an inner product with itself (
![]() )
or in
an inner product with the whitened data point
)
or in
an inner product with the whitened data point
![]() .
Thus, we can represent these two quantities
regardless of the dimensionality of the vector space using at most two
degrees of freedom: the magnitude of
.
Thus, we can represent these two quantities
regardless of the dimensionality of the vector space using at most two
degrees of freedom: the magnitude of ![]() and the
cosine of the angle between the vectors
and the
cosine of the angle between the vectors ![]() and
and ![]() .
Let us now denote the new variables as follows:
.
Let us now denote the new variables as follows: ![]() is
the magnitude of
is
the magnitude of ![]() ,
,
![]() is the magnitude of
is the magnitude of ![]() and
and
![]() is the cosine of the angle between the two
vectors. We then compactly rewrite the bound as in
Equation 7.24.
is the cosine of the angle between the two
vectors. We then compactly rewrite the bound as in
Equation 7.24.
The wim is now lower bounded by the right hand side which is a
function of two free scalars ![]() and
and ![]() .
We wish to find
the maximum of the lower bound at some value of
.
We wish to find
the maximum of the lower bound at some value of ![]() and
and ![]() .
By taking derivatives of the right hand side with respect to
.
By taking derivatives of the right hand side with respect to ![]() and setting to 0, we find an extremum of the function at
and setting to 0, we find an extremum of the function at
![]() .
However, we also note that
.
However, we also note that
![]() and so
and so
![]() .
If we set
.
If we set ![]() we note that the this solution
is always greater than the
we note that the this solution
is always greater than the
![]() .
So,
the extremum we solved for was a minimum. Thus, the maximum
occurs at the ends of the interval so
.
So,
the extremum we solved for was a minimum. Thus, the maximum
occurs at the ends of the interval so
![]() .
Therefore, we
have the relationship
.
Therefore, we
have the relationship
![]() .
In other words, let
us define
.
In other words, let
us define
![]() .
The expression for wim then
simplifies into a function of 1 free variable (c) as in
Equation 7.25.
.
The expression for wim then
simplifies into a function of 1 free variable (c) as in
Equation 7.25.
For each value of ![]() we find the value of c which maximizes the
value of
we find the value of c which maximizes the
value of ![]() .
This is done offline (taking a few seconds)
using Brent's method and the result is stored in a 1D lookup table
(LUT). The values are shown in Figure 7.3(a) where we
plot the max of the g function with respect to
.
This is done offline (taking a few seconds)
using Brent's method and the result is stored in a 1D lookup table
(LUT). The values are shown in Figure 7.3(a) where we
plot the max of the g function with respect to ![]() .
Using this
table, we can immediately compute the minimum wminim by looking
up the corresponding value of
.
Using this
table, we can immediately compute the minimum wminim by looking
up the corresponding value of ![]() for the current data point and
subsequently compute the rest of the parabolic bound's parameters.
for the current data point and
subsequently compute the rest of the parabolic bound's parameters.
An example of a parabolic bound is shown in Figure 7.3(b) under a sub-component of the Qfunction. This sub-component corresponds to a single data point as we vary one gate's uni-variate mean. Many such parabolic bounds are computed (one for each data point and gate combination) and are summed to bound the Q function in its entirety.
For greater computational efficiency we compute the gradient of the
Q on the mean to get an idea of the direction of steepest
ascent. We can then know which general direction ![]() will move
towards for the next iteration. Due to whitening,
will move
towards for the next iteration. Due to whitening, ![]() starts off
at the origin and moves from there. Thus, we know if
starts off
at the origin and moves from there. Thus, we know if ![]() is
moving close towards
is
moving close towards ![]() or farther away from
it. Equivalently, we know if c will be positive or negative. The
above LUT (Figure 7.3(a)) returns the wminim which
is valid for all possible choices of c. However, if we know the
direction c is going to move along, we only need to consider half of
the possibilities in using Brent's method to find the max of
or farther away from
it. Equivalently, we know if c will be positive or negative. The
above LUT (Figure 7.3(a)) returns the wminim which
is valid for all possible choices of c. However, if we know the
direction c is going to move along, we only need to consider half of
the possibilities in using Brent's method to find the max of
![]() .
Thus, we obtain two LUTs for c positive and for cnegative as shown in Figure 7.4(a). This
typically gives us an even tighter bound since we only need to bound
the Q function in regions of the landscape where the locus of the
maximum could move to. Thus, we are effectively approximating the
landscape with two parabolas, which are cut at c=0. One is a bound
for the values at c<0 and one for
c>0. Figure 7.4(b) depicts this piece wise
parabolic bound on a sub-component of Q. The function being bounded
is represented with a continuous line. One parabola is composed of 'x'
symbols and is a valid bound to the right of zero. The other parabola
is composed of 'o' symbols and is valid to the left of zero. The
piece-wise bound is composed of these two parabolas spliced at the
origin (their continuations are shown as dotted lines for
visualization). Thus, if the gradient tells us that we will be moving
in a direction of increasing
.
Thus, we obtain two LUTs for c positive and for cnegative as shown in Figure 7.4(a). This
typically gives us an even tighter bound since we only need to bound
the Q function in regions of the landscape where the locus of the
maximum could move to. Thus, we are effectively approximating the
landscape with two parabolas, which are cut at c=0. One is a bound
for the values at c<0 and one for
c>0. Figure 7.4(b) depicts this piece wise
parabolic bound on a sub-component of Q. The function being bounded
is represented with a continuous line. One parabola is composed of 'x'
symbols and is a valid bound to the right of zero. The other parabola
is composed of 'o' symbols and is valid to the left of zero. The
piece-wise bound is composed of these two parabolas spliced at the
origin (their continuations are shown as dotted lines for
visualization). Thus, if the gradient tells us that we will be moving
in a direction of increasing ![]() ,
we should compute the parabola
made of 'x' symbols. However, if we are moving to the left (because of
the sum total influence of the other bounds and functions), we should
use the parabola made of 'o' symbols which is a wider and tighter
bound.
,
we should compute the parabola
made of 'x' symbols. However, if we are moving to the left (because of
the sum total influence of the other bounds and functions), we should
use the parabola made of 'o' symbols which is a wider and tighter
bound.
To obtain a final answer for the update of the gate means ![]() we
simply maximize the sum of parabolas which bounds the Q in its
entirety. For M gates and N data points, we obtain
we
simply maximize the sum of parabolas which bounds the Q in its
entirety. For M gates and N data points, we obtain
![]() parabolas each with its own (
parabolas each with its own (
![]() ). The
update is in Equation 7.26.
). The
update is in Equation 7.26.