



Next: Bounding Scalars: The Gate
Up: CEM for Gaussian Mixture
Previous: Updating the Experts
Unlike the experts which can be bounded with EM and reduce to
logarithms of Gaussians, the gates can not be as easily differentiated
and set to 0. They are bounded by Jensen and the
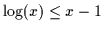 bounding and the Gaussians of the gates do not reside nicely
within a logarithm. In fact, additional bounding operations are
sometimes necessary and thus, it is important to break down the
optimization of the gates. We shall separately consider the mixing
proportions (
bounding and the Gaussians of the gates do not reside nicely
within a logarithm. In fact, additional bounding operations are
sometimes necessary and thus, it is important to break down the
optimization of the gates. We shall separately consider the mixing
proportions (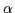 ), the means (
), the means (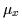 )
and the covariances
(
)
and the covariances
(
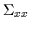 ). This separation facilitates our derivation but the
trade-off is that each iteration involves 4 steps: 1) optimize the
experts, 2) optimize the gate mixing proportions, 3) optimize the gate
means and 4) optimize the gate covariances7.1. This ECM-type [41]
approach may seem cumbersome and theoretically we would like to
maximize all simultaneously. However, the above separation yields a
surprisingly efficient implementation and in practice the numerical
computations converge efficiently.
). This separation facilitates our derivation but the
trade-off is that each iteration involves 4 steps: 1) optimize the
experts, 2) optimize the gate mixing proportions, 3) optimize the gate
means and 4) optimize the gate covariances7.1. This ECM-type [41]
approach may seem cumbersome and theoretically we would like to
maximize all simultaneously. However, the above separation yields a
surprisingly efficient implementation and in practice the numerical
computations converge efficiently.
Tony Jebara
1999-09-15