

Next: Modelling Trajectory as a
Up: Uniform Motion of Points
Previous: Uniform Velocity
We now derive relationships between points when they move with constant
acceleration. Let 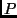 be a 3D world point,
moving with uniform linear acceleration. Let its position at any time
instant
be a 3D world point,
moving with uniform linear acceleration. Let its position at any time
instant 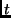 be given by
be given by
 |
(7) |
where 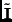 is the initial position of the point,
is the initial position of the point, 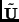 is its
initial velocity and
is its
initial velocity and
![\( \tilde{\bf A} = \left [ \begin{array}{cccc} A_x & A_y &
A_z & 1\end{array} \right ]^{\sc T}\)](img39.png) is its constant acceleration.
is its constant acceleration.
Proceeding the same way as in the previous subsection, we get
a singular matrix 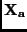
A similar singular matrix 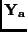 with motion parameters in
with motion parameters in
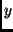 -direction also exists.
-direction also exists.
Expanding 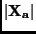 and
and 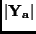 , we get
, we get
where 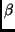 's depend only on the parameters of motion of the 3D points
in the world. The above relations are time-dependent and
view-independent. That is, the same
's depend only on the parameters of motion of the 3D points
in the world. The above relations are time-dependent and
view-independent. That is, the same 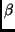 's hold no matter what the
pose and intrinsic parameters of the affine camera used to view them.
There are 16 unknowns (
's hold no matter what the
pose and intrinsic parameters of the affine camera used to view them.
There are 16 unknowns (
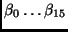 ) in the above
relation, with each time instant providing 2 equations. We, therefore,
need the velocities of 4 points for 8 time instants (9 frames) for
computing the
) in the above
relation, with each time instant providing 2 equations. We, therefore,
need the velocities of 4 points for 8 time instants (9 frames) for
computing the 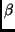 's. Note that these
's. Note that these 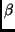 's can be computed from
a single view, as opposed to the
's can be computed from
a single view, as opposed to the  's for the case of constant
velocity, which needed two views. This is the direct result of
time-dependence.
's for the case of constant
velocity, which needed two views. This is the direct result of
time-dependence.
We now proceed to derive time-independent constraints for the case of
constant linear acceleration in the world. For this, we differentiate the
constant acceleration motion equation (Equation. 7) twice to
get
![$\displaystyle a_x = {\bf m_{1}}. \left [ \begin{array}{ccc} A_x & A_y & A_z \end{array} \right]$](img56.png) |
|
|
(10) |
![$\displaystyle a_y = {\bf m_{2}}. \left [ \begin{array}{ccc} A_x & A_y & A_z \end{array} \right]$](img57.png) |
|
|
(11) |
where 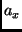 and
and 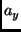 are the image-accelerations of the projection
of the point. We can similarly define the singular matrices
are the image-accelerations of the projection
of the point. We can similarly define the singular matrices
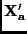 and
and
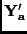 for
the four points
for
the four points 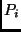 ,
,  .
.
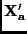 is given below.
is given below.
![$\displaystyle {\bf X_a^\prime} = \left [ \begin{array}{cccc}
A_{1x} & A_{1y} & ...
...3y} & A_{3z} & a_{3x} \\
A_{4x} & A_{4y} & A_{4z} & a_{4x}
\end{array} \right]$](img64.png) |
|
|
(12) |
Expanding the determinants of
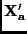 and
and
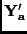 , we get
, we get
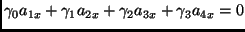 |
|
|
|
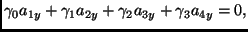 |
|
|
(13) |
where 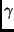 's are functions of world accelerations parameters of the 4
points only. The
's are functions of world accelerations parameters of the 4
points only. The 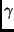 's are view and time independent. The system of
Equations 13 has four unknowns and we need 2
views of the 4 points to determine all the
's are view and time independent. The system of
Equations 13 has four unknowns and we need 2
views of the 4 points to determine all the 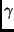 's.
's.
Levin et al. [11] derive constraints for
motion constrained to elliptic paths. It is the first time that view or
time independent constraints for points moving with constant linear
acceleration have been derived.


Next: Modelling Trajectory as a
Up: Uniform Motion of Points
Previous: Uniform Velocity
2002-10-10
![]() be a 3D world point,
moving with uniform linear acceleration. Let its position at any time
instant
be a 3D world point,
moving with uniform linear acceleration. Let its position at any time
instant ![]() be given by
be given by
![]()
![]() and
and ![]() , we get
, we get
![]() and
and
![]() , we get
, we get