

Next: Uniform Acceleration
Up: Uniform Motion of Points
Previous: Uniform Motion of Points
Let 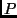 be a 3D world point, moving with uniform linear velocity. Let
be a 3D world point, moving with uniform linear velocity. Let
![${\bf I} = \left [ \begin{array}{ccc} I_x & I_y & I_z
\end{array} \right]^{\sc T}$](img2.png) be its initial position and
be its initial position and
![\({\bf U} = \left [ \begin{array}{ccc} U_x & U_y & U_z \end {array} \right]
^{\sc T}\)](img3.png) be its world velocity. These vectors are
represented as homogeneous vectors
be its world velocity. These vectors are
represented as homogeneous vectors
![\(\tilde{\bf I} = \left [
\begin{array}{cccc} I_x & I_y & I_z & 1\end{array}\right]^{\sc T}\)](img4.png) and
and
![\(\tilde{\bf U} = \left [ \begin{array}{cccc} U_x & U_y & U_z & 0 \end
{array} \right ]^{\sc T}\)](img5.png) . Its position at any time instant
. Its position at any time instant 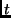 is given by
is given by
 |
(1) |
Let an affine camera observe the motion of the point. Let
![$p = \left [
\begin{array}{ccc} x & y & 1 \end{array} \right]^{\sc T}$](img8.png) be the projection
of
be the projection
of 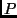 due to the affine camera matrix
due to the affine camera matrix
![${\bf M} = \left [ \begin{array}{cc}
{\bf m_{1}} & m_{14} \\
{\bf m_{2}} & m_{24} \\
{\bf0} & 1
\end{array} \right ]$](img9.png) .
where
.
where 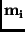 represents a vector of the first three elements in the
represents a vector of the first three elements in the 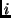 th row of
th row of 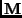 .
Then,
.
Then,
 |
(2) |
Differentiating with respect to 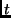 , we get
, we get
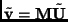 where
where
![$\tilde{\bf v} = [v_x, v_y, 0]^{\sc T}$](img15.png) is the velocity vector in
the image. This implies that the velocity of
a point in the image is a projection of the world velocity. The above
can be expanded as
is the velocity vector in
the image. This implies that the velocity of
a point in the image is a projection of the world velocity. The above
can be expanded as
![$\displaystyle v_x = {\bf m_{1}} .\left [ \begin{array}{ccc} U_x & U_y & U_z \end{array}\right ]$](img16.png) |
|
|
(3) |
![$\displaystyle v_y = {\bf m_{2}} . \left [ \begin{array}{ccc} U_x & U_y & U_z \end{array} \right ]$](img17.png) |
|
|
(4) |
Equations 3 and 4
can be written as
and
If we have 4 points in the scene,
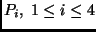 ,
with world velocities
,
with world velocities
![\( \left [ \begin{array}{ccc} U_{ix} & U_{iy} &
U_{iz} \end{array} \right]^{\sc T}\)](img21.png) and image velocities
and image velocities
![\(\left
[\begin{array}{cc} v_{ix} & v_{iy} \end{array} \right ]^{\sc T}\)](img22.png) , we can
define a matrix
, we can
define a matrix 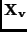 as
as
![$\displaystyle {\bf X_v} = \left [ \begin{array}{cccc}
U_{1x} & U_{1y} & U_{1z} ...
...3y} & U_{3z} & v_{3x} \\
U_{4x} & U_{4y} & U_{4z} & v_{4x}
\end{array} \right]$](img24.png) |
|
|
(5) |
Similarly, we can define a matrix 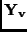 with the last column having the
velocity vectors in
with the last column having the
velocity vectors in 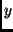 -direction. We can see that
-direction. We can see that
For these to have a constraint, 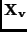 and
and 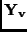 must be rank deficient,
i.e.,
must be rank deficient,
i.e.,
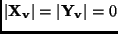 . We get the following functions of the
velocities of the 3D points and the image velocities by expanding the
expressions for the determinants.
. We get the following functions of the
velocities of the 3D points and the image velocities by expanding the
expressions for the determinants.
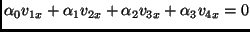 |
|
|
|
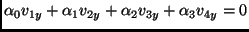 |
|
|
(6) |
where 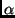 's depend only on the world velocity parameters of the 4
points. The
's depend only on the world velocity parameters of the 4
points. The 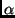 's are view-independent. That is, the above
constraints hold for the image velocities of four points for the same
's are view-independent. That is, the above
constraints hold for the image velocities of four points for the same
 's irrespective of the pose and intrinsic parameters of the
camera. They are also time-independent as time term has been
eliminated. Equation 6 has four unknowns,
with each view providing two equalities. Therefore, we need two views of
the four points to determine all
's irrespective of the pose and intrinsic parameters of the
camera. They are also time-independent as time term has been
eliminated. Equation 6 has four unknowns,
with each view providing two equalities. Therefore, we need two views of
the four points to determine all  's up to scale.
's up to scale.
These results are similar to the Recognition Polynomials and Shape
Tensors presented or discovered earlier. It was shown that polynomials to
recognize a configuration of stationary points could be constructed from
2 views of 4 points under orthographic
projections [1]. This was extended to recognize human
gait using 2 views of 5 points under scaled-orthographic
projections [2]. Time-dependent constraints involving
a single view of 5 points with uniform velocity is presented
in [11] for affine projection.. Our
results yield view and time independent constraints involving 4 points in
2 views under the general affine projection.


Next: Uniform Acceleration
Up: Uniform Motion of Points
Previous: Uniform Motion of Points
2002-10-10
![]() be a 3D world point, moving with uniform linear velocity. Let
be a 3D world point, moving with uniform linear velocity. Let
![]() be its initial position and
be its initial position and
![]() be its world velocity. These vectors are
represented as homogeneous vectors
be its world velocity. These vectors are
represented as homogeneous vectors
![]() and
and
![]() . Its position at any time instant
. Its position at any time instant ![]() is given by
is given by
![${\bf M} = \left [ \begin{array}{cc}
{\bf m_{1}} & m_{14} \\
{\bf m_{2}} & m_{24} \\
{\bf0} & 1
\end{array} \right ]$](img9.png) .
where
.
where