

Next: General Planar Motion
Up: Frame Alignment
Previous: Frame Alignment
If we can identify points
moving with constant acceleration, Equations 8
and 9 would hold for both views for the same
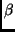 's. The time
's. The time 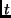 can be replaced with the frame number. From the
image velocities of the projections of 4 points in 8 frames in view
can be replaced with the frame number. From the
image velocities of the projections of 4 points in 8 frames in view 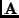 ,
, 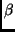 's that characterize the point configuration can be
computed. We want to identify the corresponding frame
's that characterize the point configuration can be
computed. We want to identify the corresponding frame 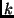 in view
in view 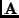 for the frame
for the frame 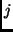 in view
in view 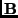 . The image velocities of the
projections of the four points in view
. The image velocities of the
projections of the four points in view 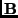 at time instant
at time instant 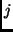 are
(
are
(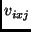 ,
,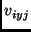 ),
), 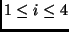 . Therefore, the shift is
. Therefore, the shift is 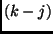 . We
have
. We
have
And a similar relation in 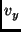 values. These can be written as
values. These can be written as
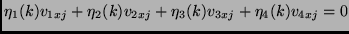 |
|
|
|
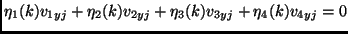 |
|
|
(21) |
where
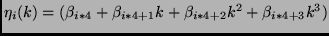 ,
, 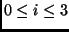 . We can solve for
. We can solve for 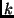 using a
linear least squares solution technique by minimizing the sum of squares
of the error functions
using a
linear least squares solution technique by minimizing the sum of squares
of the error functions
Alternately, we can solve for the roots of a cubic polynomial of the form
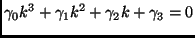 |
|
|
(22) |
where
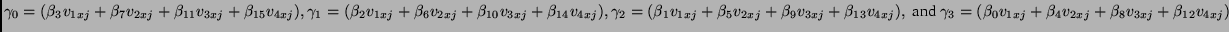 .
.


Next: General Planar Motion
Up: Frame Alignment
Previous: Frame Alignment
2002-10-10