

Next: Experimental Results
Up: Frame Alignment
Previous: Uniform Acceleration Motion:
Figure 1:
Two image sequences of an exploding pot
 |
If points undergoing general planar motion can be tracked across time,
the trajectory of each forms a contour which is viewed by both video
cameras. Both videos see the same contour, but the starting points are
different. The problem reduces to contour matching under affine
homography and unknown shift. Solutions for this situation using a
measure similar to 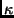 has been presented in [10].
The new measure is
has been presented in [10].
The new measure is
where p is a constant (typically 1 or 2) and 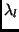 is the unknown
shift in view
is the unknown
shift in view 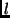 compared to the reference view
compared to the reference view  . The ratio
. The ratio
![$\frac{\kappa^{\prime}_p(l)[k]}{\kappa^{\prime}_p(0)[k]}$](img123.png) will be a
complex sinusoid. The shift
will be a
complex sinusoid. The shift 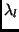 can be recovered from the inverse
Fourier transform of this ratio. For more details, see [10].
can be recovered from the inverse
Fourier transform of this ratio. For more details, see [10].
2002-10-10

![$\displaystyle ({\bf X}^l[k])^{*{\sc T}}
\left[ \begin{array}{cl} 0 & 1 -1\;\; & 0 \end{array}\right] {\bf X}^l[p]$](img120.png)