



Next: P3P - Fitting the
Up: Face Normalization and Recognition
Previous: Generating the Average 3D
It is essential to fit the 3D range data of the mean face so that it models a
face found in a 2D image. Assume we have a 2D image with the coordinates of
the eyes, the nose and the mouth perfectly pinpointed, as in
Figure ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . Denote the 2D positions of the eyes, nose and mouth
as
. Denote the 2D positions of the eyes, nose and mouth
as
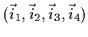 .
The parameters of the 3D
model
.
The parameters of the 3D
model
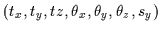 must be
tuned to align its 3D anchor points
must be
tuned to align its 3D anchor points
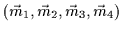 so that their 2D projections
coincide with the set of 2D anchor points
so that their 2D projections
coincide with the set of 2D anchor points
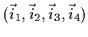 .
Note that the alignment to the
destination points
.
Note that the alignment to the
destination points
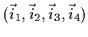 involves
minimizing 8 distances since each of these points is a 2D position. We observe
that Equation
involves
minimizing 8 distances since each of these points is a 2D position. We observe
that Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) , which only has 7 degrees of freedom, is
over-specified. Thus, there is usually no exact solution to the fitting
problem, only approximations.
, which only has 7 degrees of freedom, is
over-specified. Thus, there is usually no exact solution to the fitting
problem, only approximations.
Figure 4.9:
Image of U.S. President Ford with eyes, nose and mouth located
 |
Tony Jebara
2000-06-23

![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . Denote the 2D positions of the eyes, nose and mouth
as
. Denote the 2D positions of the eyes, nose and mouth
as
![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) , which only has 7 degrees of freedom, is
over-specified. Thus, there is usually no exact solution to the fitting
problem, only approximations.
, which only has 7 degrees of freedom, is
over-specified. Thus, there is usually no exact solution to the fitting
problem, only approximations.