



Next: Intersection of Lines of
Up: Real-Time Symmetry Transform
Previous: Real-Time Symmetry Transform
The computation of lines of symmetry begins with the concept of cocircular
edges. A pair of edges is cocircular if a circle can be constructed with each
edge as a tangent. Furthermore, if a line is drawn connecting the centers of
the edges, the angle formed between this line and each edge's tangent is the
same. We define the point of cocircularity as the center of the circle
(xc,yc) and its radius rc is the radius of cocircularity, as
indicated in Figure ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . Note that
. Note that
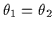 in the
figure.
in the
figure.
Figure 2.7:
Cocircularity of edges
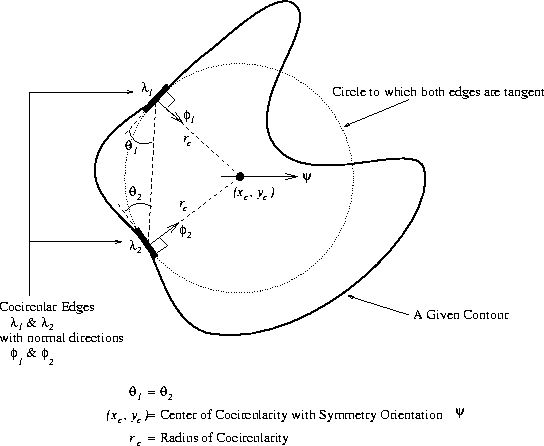 |
Furthermore, the center of cocircularity has an orientation associated with
it. This orientation is determined by the phase of the cocircular edges
contributing to this center of cocircularity. The phase value of an edge is
the orientation of the normal of the edge. This normal points along the
direction of the change of intensity from dark to bright. As displayed in
Figure ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) , the edges have phases
, the edges have phases 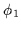 and
and 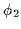 which are computed from the Sobel edge detection. The symmetry orientation at
the center of cocircularity,
which are computed from the Sobel edge detection. The symmetry orientation at
the center of cocircularity, 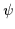 ,
is the line that bisects the normals of
the two edges. Equation
,
is the line that bisects the normals of
the two edges. Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) returns the value of
returns the value of 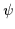 .
.
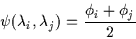 |
(2.1) |
The lines of symmetry are formed by linking all centres of circularity found
in the image. In other words, circles are constructed from all pairs of
cocircular edges and their centers (the centers of cocircularity) are used to
trace out lines of symmetry. For each point
p=(xc,yc) in the image, we
consider the surrounding neighbourhood of radius
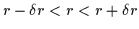 .
The range of r forms a ring shaped, circular annular region. Within that
region, we consider all pairs of edges which have a center of cocircularity at
p. We shall denote this set of cocircular edges as
.
The range of r forms a ring shaped, circular annular region. Within that
region, we consider all pairs of edges which have a center of cocircularity at
p. We shall denote this set of cocircular edges as
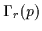 .
We
further constrain this set of cocircular edges such that only cocircular edges
with a symmetry orientation of
.
We
further constrain this set of cocircular edges such that only cocircular edges
with a symmetry orientation of
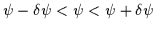 are
considered. Thus, this subset of edges in the neighbourhood of p is denoted
as
are
considered. Thus, this subset of edges in the neighbourhood of p is denoted
as
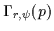 .
.
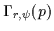 will be used to refer to the set
of all pairs of cocircular edges
will be used to refer to the set
of all pairs of cocircular edges
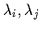 with center of
circularity at p with radius of cocircularity
with center of
circularity at p with radius of cocircularity
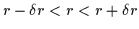 and with orientation of symmetry
and with orientation of symmetry
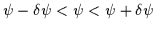 .
.
Furthermore, the centers of cocircularity can be assigned different strengths
depending upon the orientation of the edges and the intensity of the edges
that contribute to forming them. For each point in the image p, at each
scale or radius r and for each symmetry orientation 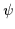 we find the set
of cocircular pairs of edges
we find the set
of cocircular pairs of edges
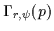 .
Sela defines the
magnitude of symmetry in the (p, r,
.
Sela defines the
magnitude of symmetry in the (p, r, 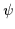 )
space as follows:
)
space as follows:
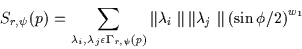 |
(2.2) |
where
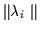 and
and
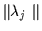 are the edge intensities of the two circular edges and
are the edge intensities of the two circular edges and 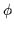 is the angle
separating their normals:
is the angle
separating their normals:
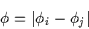 |
(2.3) |
Cocircular edges with a larger value of
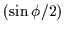 ,
increasingly face
and oppose each other and a stronger sense of symmetry is perceived at the
point of cocircularity, p. The parameter w1 is used to attenuate or
boost the effect of
,
increasingly face
and oppose each other and a stronger sense of symmetry is perceived at the
point of cocircularity, p. The parameter w1 is used to attenuate or
boost the effect of
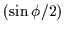 .
Selecting a large w1 will diminish
the contribution of non-facing edges so that only opposing cocircular edges
will trigger
.
Selecting a large w1 will diminish
the contribution of non-facing edges so that only opposing cocircular edges
will trigger
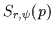 .
A value of w1=5 is proposed by Sela
[42].
.
A value of w1=5 is proposed by Sela
[42].
Thus, the magnitude of the symmetry
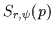 at each point p, at
each radius r and at each orientation
at each point p, at
each radius r and at each orientation 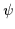 is obtained and represents the
desired ``lines of symmetry''. It is possible to combine the lines of symmetry
from multiple radii so that an overall, r-independent value of
is obtained and represents the
desired ``lines of symmetry''. It is possible to combine the lines of symmetry
from multiple radii so that an overall, r-independent value of
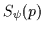 is found as follows:
is found as follows:
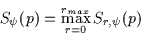 |
(2.4) |
Note that these lines of symmetry are not really lines. Rather, we compute a
symmetry magnitude at each combination of p, r and 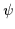 so the result is
a set of points with an orientation value. If true connected lines are
required, these discrete points must be linked into curves using their
orientation and scale value (see Chapter 3).
so the result is
a set of points with an orientation value. If true connected lines are
required, these discrete points must be linked into curves using their
orientation and scale value (see Chapter 3).




Next: Intersection of Lines of
Up: Real-Time Symmetry Transform
Previous: Real-Time Symmetry Transform
Tony Jebara
2000-06-23

![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) . Note that
. Note that
![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) , the edges have phases
, the edges have phases ![]() and
and ![]() which are computed from the Sobel edge detection. The symmetry orientation at
the center of cocircularity,
which are computed from the Sobel edge detection. The symmetry orientation at
the center of cocircularity, ![]() ,
is the line that bisects the normals of
the two edges. Equation
,
is the line that bisects the normals of
the two edges. Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) returns the value of
returns the value of ![]() .
.
![]() we find the set
of cocircular pairs of edges
we find the set
of cocircular pairs of edges
![]() .
Sela defines the
magnitude of symmetry in the (p, r,
.
Sela defines the
magnitude of symmetry in the (p, r, ![]() )
space as follows:
)
space as follows:
![]() at each point p, at
each radius r and at each orientation
at each point p, at
each radius r and at each orientation ![]() is obtained and represents the
desired ``lines of symmetry''. It is possible to combine the lines of symmetry
from multiple radii so that an overall, r-independent value of
is obtained and represents the
desired ``lines of symmetry''. It is possible to combine the lines of symmetry
from multiple radii so that an overall, r-independent value of
![]() is found as follows:
is found as follows:
![]() so the result is
a set of points with an orientation value. If true connected lines are
required, these discrete points must be linked into curves using their
orientation and scale value (see Chapter 3).
so the result is
a set of points with an orientation value. If true connected lines are
required, these discrete points must be linked into curves using their
orientation and scale value (see Chapter 3).