



Next: Real-Time Implementation
Up: Real-Time Symmetry Transform
Previous: Lines of Symmetry
Sela proposes that the intersection of the lines of symmetry in
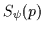 generates an interest point. This interest point has a magnitude depending on
the configuration and strength of the lines of symmetry that generated it. We
utilize the magnitude of the interest point as a measure of the level of
symmetric enclosure at that point. Since perpendicular lines of symmetry
generate the strongest sense of enclosure [42], the greater the level
of orthogonality between two lines of symmetry, the stronger their
contribution to the interest magnitude at point p. The contribution of each
pair of lines of symmetry intersecting point p is summed to generate an
interest value I(p) which is defined as
generates an interest point. This interest point has a magnitude depending on
the configuration and strength of the lines of symmetry that generated it. We
utilize the magnitude of the interest point as a measure of the level of
symmetric enclosure at that point. Since perpendicular lines of symmetry
generate the strongest sense of enclosure [42], the greater the level
of orthogonality between two lines of symmetry, the stronger their
contribution to the interest magnitude at point p. The contribution of each
pair of lines of symmetry intersecting point p is summed to generate an
interest value I(p) which is defined as
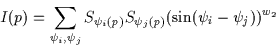 |
(2.5) |
where
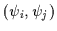 are the orientation values of a pair of symmetry
lines intersecting point p whose symmetry magnitudes are
are the orientation values of a pair of symmetry
lines intersecting point p whose symmetry magnitudes are
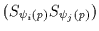 .
The effect of orthogonality is included in the
.
The effect of orthogonality is included in the
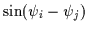 term which is maximal when the lines of symmetry are
perpendicular. The weight w2 is used to tune the sensitivity of the
computation to the orthogonality of the intersecting lines of symmetry. A
value of w2=5 is typically used so that orthogonal lines of symmetry
dominate the response of the interest operator.
term which is maximal when the lines of symmetry are
perpendicular. The weight w2 is used to tune the sensitivity of the
computation to the orthogonality of the intersecting lines of symmetry. A
value of w2=5 is typically used so that orthogonal lines of symmetry
dominate the response of the interest operator.




Next: Real-Time Implementation
Up: Real-Time Symmetry Transform
Previous: Lines of Symmetry
Tony Jebara
2000-06-23