



Next: Updating the Gates
Up: CEM for Gaussian Mixture
Previous: CEM for Gaussian Mixture
To update the experts, we hold the gates fixed and merely take
derivatives with respect to the expert parameters
(
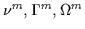 or call them
or call them
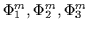 ). This derivative is simplified and set
equal to zero as in Equation 7.17. This is our
update equation for the experts. Note how each expert has been
decoupled from the other experts, from the gates and from other
distracting terms. The maximization reduces to the derivative of the
logarithm of a single conditioned Gaussian. This can be done
analytically with some matrix differential theory and, in fact, the
computation resembles a conditioned Gaussian maximum-likelihood
estimate in Equation 7.18 [37]. The
responsibilities for the assignments are the standard normalized joint
responsibilities (as in EM). The update equation is effectively the
maximum conditional likelihood solution for a conditioned multivariate
Gaussian distribution.
). This derivative is simplified and set
equal to zero as in Equation 7.17. This is our
update equation for the experts. Note how each expert has been
decoupled from the other experts, from the gates and from other
distracting terms. The maximization reduces to the derivative of the
logarithm of a single conditioned Gaussian. This can be done
analytically with some matrix differential theory and, in fact, the
computation resembles a conditioned Gaussian maximum-likelihood
estimate in Equation 7.18 [37]. The
responsibilities for the assignments are the standard normalized joint
responsibilities (as in EM). The update equation is effectively the
maximum conditional likelihood solution for a conditioned multivariate
Gaussian distribution.
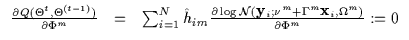 |
|
|
(7.17) |
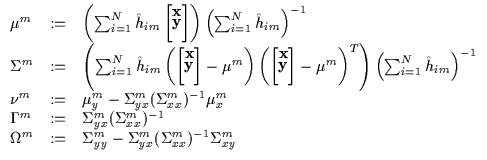 |
|
|
(7.18) |
We observe monotonic increases when the above maximization is iterated
with the bounding step (i.e. estimation of
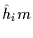 ). This result
is not too surprising since we are effectively applying a version of
EM to update the experts. At this point, we turn our attention to
the still unoptimized gates and mixing proportions.
). This result
is not too surprising since we are effectively applying a version of
EM to update the experts. At this point, we turn our attention to
the still unoptimized gates and mixing proportions.




Next: Updating the Gates
Up: CEM for Gaussian Mixture
Previous: CEM for Gaussian Mixture
Tony Jebara
1999-09-15
![]() ). This result
is not too surprising since we are effectively applying a version of
EM to update the experts. At this point, we turn our attention to
the still unoptimized gates and mixing proportions.
). This result
is not too surprising since we are effectively applying a version of
EM to update the experts. At this point, we turn our attention to
the still unoptimized gates and mixing proportions.