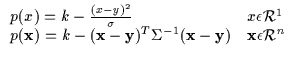 |
(6.3) |
In the above, the parabola contains a maximum which is the scalar
value k. It also contains a locus for the maximum which is ![]() (an element in n-dimensional Euclidean space). Finally, it contains a shape
parameter,
(an element in n-dimensional Euclidean space). Finally, it contains a shape
parameter, ![]() (or
(or ![]() in 1 dimension) which is a symmetric
positive semi-definite matrix. There are simpler forms for the bound
p (such as a constant or linear function) however the above bound is
flexible because it has a single arbitrary maximum, k, at an
arbitrary locus,
in 1 dimension) which is a symmetric
positive semi-definite matrix. There are simpler forms for the bound
p (such as a constant or linear function) however the above bound is
flexible because it has a single arbitrary maximum, k, at an
arbitrary locus, ![]() .
In addition, the maximization of a quadratic
bound is straightforward and the maximization of a sum of quadratic
bounds involves only linear computation. In addition, unlike
variational bounds, the bounding principles used here do not
necessarily come from the dual functions (i.e. linear tangents for
logarithms, etc.) and are always concave paraboloids which are easy to
manipulate and differentiate
[53] [51]. Higher order functions and other
forms which may be more flexible than quadratics are also usually more
difficult to maximize.
.
In addition, the maximization of a quadratic
bound is straightforward and the maximization of a sum of quadratic
bounds involves only linear computation. In addition, unlike
variational bounds, the bounding principles used here do not
necessarily come from the dual functions (i.e. linear tangents for
logarithms, etc.) and are always concave paraboloids which are easy to
manipulate and differentiate
[53] [51]. Higher order functions and other
forms which may be more flexible than quadratics are also usually more
difficult to maximize.