



Next: Quadratic Bounds
Up: Optimization - General Bound
Previous: Optimization - General Bound
An important tool in optimization is bounding [54]. Bounding
can be used to compute upper or lower bounds on functions,
approximation errors, etc. to tackle intractable maximization or
minimization problems. The principles of bounding are central in
variational methods which utilize bounds as approximation and
optimization tools [53] [51]. Of particular
relevance are applications in statistics and graphical model learning
as discussed by Rustagi [53] and Jordan
[29]. An interesting application is shown by
Jaakkola [25] where bounds on Bayesian Networks are
introduced to reduce intractable computations in a graphical model. We
will discuss bounding techniques in a slightly different way,
emphasizing quadratic bounds as opposed to the dual bounds typical of
variational techniques and we occasionally refer back to some ideas
used by classical variational methods in the literature.
Let us consider the usefulness of a bound for arbitrary function
optimization. 6.1 Take a function, f, which maps a scalar, x, to a scalar,
i.e.
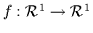 .
For bounding purposes, the
function's domain need not be restricted to this space and can be
directly extended to
.
For bounding purposes, the
function's domain need not be restricted to this space and can be
directly extended to
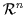 and some non-Euclidean spaces as
well. Now consider consider p which we shall call our contacting
lower bound of f because of the properties in
Equation 6.1.
and some non-Euclidean spaces as
well. Now consider consider p which we shall call our contacting
lower bound of f because of the properties in
Equation 6.1.
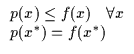 |
|
|
(6.1) |
It can be shown that increasing p will also increase f as in
Equation 6.2. This is a trivial proof however it
guarantees that iteratively optimizing a function's bound is a useful
alternative to directly optimizing the function. In the following, we
can see that if we are currently operating at a point x* on
function f, maximizing the bound p underneath f will make us
move to another locus, x** where f is increased.
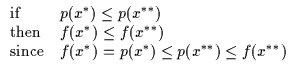 |
|
|
(6.2) |




Next: Quadratic Bounds
Up: Optimization - General Bound
Previous: Optimization - General Bound
Tony Jebara
1999-09-15
![]() .
For bounding purposes, the
function's domain need not be restricted to this space and can be
directly extended to
.
For bounding purposes, the
function's domain need not be restricted to this space and can be
directly extended to
![]() and some non-Euclidean spaces as
well. Now consider consider p which we shall call our contacting
lower bound of f because of the properties in
Equation 6.1.
and some non-Euclidean spaces as
well. Now consider consider p which we shall call our contacting
lower bound of f because of the properties in
Equation 6.1.