 |
Recall that the large vectors Y(t) represent a full window of past
interaction (short term memory). This window effectively covers
![]() seconds of temporal data. This data is weighted
with an exponential decay which scales down
seconds of temporal data. This data is weighted
with an exponential decay which scales down ![]() vectors that
constitute the big Y(t) vector. The further back in time a
vectors that
constitute the big Y(t) vector. The further back in time a ![]() component is, the more its amplitude is attenuated. Thus, an
exponential ramp function is multiplied with each Y window (i.e. a
few seconds of each of the 30 time series). This reflects our
intuition that the more temporally distant the elements in the time
series, the less relevant they are for prediction. This decay agrees
with some aspects of cognitive models obtained from psychological
studies [16]. Once the vectors have been attenuated,
they form a new 'exponentially decayed' short term memory window
component is, the more its amplitude is attenuated. Thus, an
exponential ramp function is multiplied with each Y window (i.e. a
few seconds of each of the 30 time series). This reflects our
intuition that the more temporally distant the elements in the time
series, the less relevant they are for prediction. This decay agrees
with some aspects of cognitive models obtained from psychological
studies [16]. Once the vectors have been attenuated,
they form a new 'exponentially decayed' short term memory window
![]() .
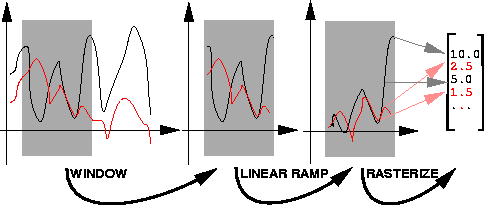
The process is shown in Figure 4.4
where a window is placed over the time series, generating a short term
memory Y. An exponential decay function is used to decay it and
generates the
.
The process is shown in Figure 4.4
where a window is placed over the time series, generating a short term
memory Y. An exponential decay function is used to decay it and
generates the ![]() version. The eigenspace previously discussed
is really formed over the
version. The eigenspace previously discussed
is really formed over the ![]() distribution and representing
distribution and representing
![]() in only this subspace (i.e. the top eigenvectors) generates
the compact vector
in only this subspace (i.e. the top eigenvectors) generates
the compact vector
![]() .
This is the final, low dimensional
representation of the gestural interaction between the two humans over
the past few seconds.
.
This is the final, low dimensional
representation of the gestural interaction between the two humans over
the past few seconds.