The Othello Project
Juno Suk, jsuk@lucent.com

Introduction
In this project, we are given an Othello game written in Java with a genetic programming implementation already in place. This original implementation consists of 13 primitives, + - * / 10 black black_corners black_near_corners black_edges white white_corners white_near_corners white_edges. The first four primitives are standard arithmetic operators while the rest of the primitives are terminals, all but one corresponding to positions on the board. All the standard genetic programming population control constructs such as crossover, mutation, and ADFs are included in the given Java package, gpjpp. In addition to this genetic programming setup, a computer player, EDGAR, is provided. Though not a genetically programmed player, EDGAR boasts a superior playing ability, easily dispatching most Othello players in short time. It is the purpose of this project to modify and extend the current genetic programming setup in hopes of discovering new approachs in implementation and representation that will facilitate the creation and evolution of GP players that can play well against both EDGAR and the general othello playing population.

Approach
To begin the process of creating a competent othello player, I first surveyed the past research done on this same project to see what approaches had met with success and what approaches had not. From this survey, I came up with a couple observations that led to an interesting observation and a five part plan to create a better othello player.

An Interesting Observation
I observed that most of the papers had proven unsuccessful in getting any improved results when adding new terminal types to the primitive set. But there was one paper which stood out from the rest because it had replaced the initial set of terminals entirely with a new set of its own and had fantastic results against EDGAR as well as the general population. The paper by Chris Porcelli and Patrick Pan had results that were clearly different (they were successful) than the rest of the papers in the class, so after pondering what set their approach apart from the rest I realized a commonality among the other approaches that had been inadvertently excluded from Porcelli and Pan's approach. This was the absence of the black and the white terminals.

Taking a look at how the othello board evaluated its primitives, I was surprised to find that it had not normalized the values but rather, just gave the total sum of the pieces satisfying each primitive. That would mean the following maximum values for each primitive:
black/white 64
black_corners/white_corners 4
black_near_corners/white_near_corners 12
black_edges/white_edges 30
10 (constant) 10
As can be seen, the distribution of values among the primitives are not equal. Especially noted, the black and white primitives can easily overshadow all the other primitives with its maximum value of 64 against the other primitives' total sum of 4 + 12 + 30 + 10 = 56.

What does this mean? The effect of the potentially large valued primitive will cause the other values to play a less significant role in a GP tree and will, by evolution, become extinct. This extinction is evident in many of the class papers as their results often returned the simple tree of white or black depending on which side they trained on. And if not just the single primitive, most, if not all, of the trees incorporated these couple primitives in their trees somehow.

Why is this? Imagine a three dimensional surface representing the hypothesis space. This is admittedly not a perfect model since the hypothesis space is not being represented by only three primitives but, conceptually, it should suffice. The goal of genetic programming is to come up with a player that is found on the lowest point of this three dimensional surface- the global minimum. To find this minimum, GP creates random players scattered throughout this surface and measures their "elevation" by their fitness. The lowest elevated are combined through crossovers in hopes that the created progeny are found at a lower elevation and, ultimately, create the one that is found at the global minimum. In this way, the progeny, a.k.a. GP hypotheses, gradually converge upon the minimum. Unfortunately, there are local minima as well that occupy this hypothesis space. Now, take the primitives black and white, which by themselves are a generally good heuristic to follow, but do not represent the global minimum. But the results do show that these primitives reside at a minimum, a local one. Due to the magnitude of the primitives, the valley that this minimum lies at the bottom can be imagined to be a shallow but wide one, occupying much of the hypothesis space. Most of the hypothesis representations containing the black/white primitive will tend to fall into some part of this valley, and after a few generations, will gradually converge to the hypothesis at the bottom of the valley. The global minimum lies somewhere else on the surface but its valley is relatively small in width compared to the large valley of the black/white primitive. Therefore, between generations, hypotheses in this smaller but deeper valley are come across infrequently, and when they are found, will not likely survive once they are crossovered with another hypothesis since the other hypothesis may contain the offending primitive which will cause the offspring to fall into the wide shallow valley once again.

Also worthy of noting is the fact that these two primitives will tend to dominate later in the game when more pieces have been placed on the board. For example, take a look at this scenario: 

. . . . . . . ?

? w w w w w w b

w w w w w w . .

w w w w w . . .

w w w w w . . .

w w w w b b w .

b b . . . . b .

w . . . . . . w
As you can see, black is considering two choices. One represents a really good choice (the upper right hand corner) while the other is a terrible choice (left side, second from top). As you can see, if black takes the corner, then strategically, he sets himself up to claim several columns and top edge pieces. On the other hand, if he takes the left position, then, even though he gains many pieces, he only makes things worse since white can then claim the whole left edge including the upper left corner. Now what if the gp function was ( + ( - ( * 5 black_corner ) ( / black_near_corner 2 )) black ). Then the upper right hand choice (good choice) would give you 5 - 2 + 12 = 15. The other choice (bad choice) would give you 0 - 3 + 20 = 17. So even though it seems as though the gp function will take into consideration that you will be gaining an extra black_corner and not as many black_near_corners, it still ends up taking the left side, due to the overwhelming numbers of the black primitive.

This is exactly what should be avoided - the end game is played much more effectively when the corners/edges/near_corners become a greater factor. So the exact behavior is desired - the black/white primitives should decrease in the later game to let all the other primitives play a role. Unfortunately, this is not the case.

So the observation here is the classic "can't see over the trees to see the forest" problem. Because of the dominating white/black primitives, much of the hypothesis space is never explored and better trees in the distance cannot be discovered.

Creating A Better Othello Player: Part 1
In the first set of tests, there are two subparts.

In the first subpart, I run the genetic programming as-is. These tests will serve merely as a base reference to compare the results from other parts by.

In the second subpart, I trained the population against the (deterministic) EDGAR opponent. There is a reasoning behind this.

It is important to consider that the evolutionary process may be able to see past the dominating primitives and will boost the other primitives up by a multiplier constant. For example, the GP tree ( + white ( * 10 ( + white_corners white_corners ))) can potentially avoid the dominating effect of white. Performance results from this training will also be a base reference for later training against EDGAR.

Creating A Better Othello Player: Part 2
In this part, I again trained against both random players and EDGAR, but with one minor change. In the board evaluation, I divide the white/black values by 8. This should lessen the dominating effect of these primitives and bring them down to the level of the other primitives. Hopefully now, the population gets a chance to evolve into other areas of the hypothesis space "forest".

The only caveat now is that the black_edges/white_edges primitives are now too large with their maximum value of 30. But that is not a concern in this project since these primitives will be replaced with a new set in the next part. The purpose of this part is merely to see if the reduction of black/white will bring any sense of improvement.

Creating A Better Othello Player: Part 3
In this part, I introduce a new set of terminals. Inspired partially by the work of Patrick Pan and Chris Porcelli, and Daby Sow, this set of terminals is a sort of hybrid between their set of terminals.

In Pan and Porcelli's work, they introduce a set of 10 * 2 terminals making use of the radial semi-symmetry of the othello board. Each primitive corresponds to a unique position on the board which may occur on the board either 4 or 8 times depending on its location on the symmetrical area. Take a look at their paper to get a more comprehensive treatement of their implementation.

In Sow's work, he introduces a set of terminals that are dependent on the distance the position is from the corner. This results in a layout of primitive positions that are arranged in 4 quarter squares, each concentric to a corner of the board. Take a look at his paper for a comprehensive description.

For my new set of terminals, I borrow Daby Sow's concept of corner-distant terminals as well, but extending it further to include center-distant terminals as well. Here are diagrams of the terminal set:



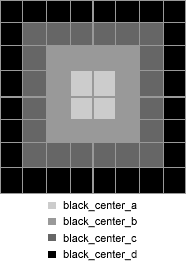
These 8 * 2 terminals (times 2 for the white terminals) allow me to be just as expressive as the 10 * 2 terminal set of Pan and Porcelli. Both terminal sets cover all the positions of the board and the 8 primitive locations in my set can represent any one of the 10 unique positions by the intersection of 1 center terminal and 1 corner terminal from my set.
It also has the added advantage of being a smaller set, leading to a smaller hypothesis space to search and, therefore, leading to faster convergence.

Taking advantage of the smaller set of terminals, I added a few constants, 5 4 3 2 as terminals to hopefully encourage the evolution in assigning weights to the different terminals.

All the terminals are normalized to a base total of 28 to avoid the "forest over the trees" problem. 

Terminal        Tiles   Factor       Total
--------------  -----   ------       ----------------
black_center_a  4	7.0          28.0
black_center_b  12      2.3          27.6
black_center_c  20      1.4          28.0
black_center_d  28      1.0          28.0

black_corner_w  4	7.0          28.0
black_corner_x  12      2.3          27.6
black_corner_y  20      1.4          28.0
black_corner_z  28      1.0          28.0
Creating A Better Othello Player: Part 4
In this part, we get down to business.

First, all training is now done as as a black player in preparation for playing against EDGAR.

The set of terminals is further reduced by removing unneeded terminals. Specifically, all the primitives related to the white player have been removed since they really aren't needed. In the process of evaluating different board positions for black, any white pieces that are removed will be reciprocated by an increase in the black pieces. And white pieces never increase when black is evaluating its options. So the black primitives' values will reflect any reductions in the white primitives' values, and, therefore, having white primitives around is redundant. Removing them can only prove beneficial since it will reduce not only the hypothesis space, but the evaluation computation time in half.

The black primitive has been reintroduced to the set since it still is an important measure to be considered. It is known now as black_total and is normalized by being multiplied by 0.4375. (0.4375 * 64 = 28)

Creating A Better Othello Player: Part 5
The last part of the five part plan, everything remains the same as in part 4 except two things:
1. Train against (deterministic) EDGAR
2. Get unbiased results
In the previous parts, results were just taken to get the general idea of how the new concept worked. But in this final part, we want to create the best possible player, not only one that can beat EDGAR but one that can generalize and play other types of players, human and random, as well. Therefore, all resulting trees were run through a validation set of 50 random players. Unfortunately, EDGAR is deterministic and plays the same each time so I couldn't use him for the validation set since he would give the same result every time. Therefore, the best GP player from each generation was validated using 50 games against the random player. The best players after validation were not run through a final testing set since they had already been run through 50 random games which should have removed most bias from playing EDGAR in itself and should not have introduced much bias itself since the validation cases were all random.

Problems
In part 3, all results were invalidated because of a bug found in my board evaluation function.

Also, a bug was found in the OthelloGPPlayer implementation provided. Any GP function containing a left parens followed by a right parens ") (" caused parsing errors. Any GP functions containing this combination may have been evaluated incorrectly by the OthelloGPPlayer. The extent of damage this had on parts 1 through 2 (and on all the previous projects using this Othello project) should be minimal though since parens really are unnecessary when processing any prefix/postfix equation since they are only there for our clarity's sake. Nevertheless, I found that the parse error did affect my OthelloCache runs against EDGAR so it may have done some damage after all. The OthelloGPPlayer was fixed during the debugging of part 3. It now strips the function of all parens since they are unnecessary. So results for parts 4 and 5 should be fine.



Results
Only the best result(s) from each training session are shown. Click on the links to view the actual output files and configuratons. Or click here to view all result sets.

Part 1

GP trained against random (set 1a)
-------------------------
Best GP function:                 white

Against black random player:      47 wins, 3 losses

Against EDGAR(white)
GP Player(black):                 WHITE 49 BLACK 15



GP trained against EDGAR (set 1c)
------------------------
Best GP function:                 ( -  ( /   white_near_corners   black )
                                       ( /   black_edges   10 ))

Against black random player:      46 wins, 4 losses

Against EDGAR(white)
GP Player(black):                 WHITE 18 BLACK 46

Part 2

GP trained against random (set 1b)
-------------------------
Best GP function:                 ( * ( - white_corners
                                          ( / white_near_corners
                                              white_near_corners ))
                                      white_edges )


Against black random player:      49 wins, 1 loss

Against EDGAR(white)
GP Player(black):                 WHITE 36 BLACK 28


GP trained against EDGAR (set 2c)
------------------------
Best GP function:                 ( -   white_corners
                                        ( /   white_edges
                                              white_edges ))

Against black random player:      49 wins, 1 loss

Against EDGAR(white)
GP Player(black):                 WHITE 16 BLACK 48

Part 3

Results for this section are invalid.
To see them anyway, go to set3a or set3b or set3c

Part 4

GP trained against random (set 4a)
-------------------------
Best GP function:                 ( + black_center_d black_corner_w )

Against white random player:      49 wins, 1 loss

Against EDGAR(white)
GP Player(black):                 WHITE 48 BLACK 16

Part 5

(set 5a set 5b)

Player  GP Function                      vs random(white)   vs EDGAR(white)
------  -------------------------------  -----------------  ----------------
1       ( -  ( *   black_corner_z  black_center_d )
             ( /   black_corner_z   5 ))

                                         50 wins, 0 losses  WHITE 3 BLACK 20



2       ( /  ( *  ( -  ( / black_corner_x black_center_c ) ( +   4   5 ))
                  ( -  ( +   5 black_center_d )
                       ( * black_center_d   4 )))  4 )

                                         49 wins, 1 loss    WHITE 0 BLACK 48



3       ( +  ( *   black_corner_w   black_corner_z )
             ( *   black_total   black_center_b ))

                                         50 wins, 0 losses  WHITE 8 BLACK 23



Conclusions
This project was successful in its main goal which was to come up with new approaches in implementation and representation in the creation of more effective genetically programmed othello players. It was also hoped that these new approaches would facilitate the development of players that could beat EDGAR and also play well against the general public. Surprisingly, this hope was fulfilled early in part 1 when the GP player evloved from training against EDGAR was able to beat EDGAR and still win 46 games out of 50 against a random player.

But the best players were unarguably evolved in the final part where the GP players were able to beat EDGAR by a landslide (48 to 0) and were still generalized enough to beat the random player 98 to 100% of the time.

But to evolve such good players at the end, there were many factors along the way that contributed to the final success. The first factor was the training factor - who to train against. In a couple papers from class, it was stated that the random player was too easy and that EDGAR was too difficult and because of the lack of mid-level players, the GP could not produce any good players for lack of a gradient. I would contest that position and point out that in the first part of my project, training against EDGAR with the primitives remaining the way they were evolved a perfectly capable player who could beat EDGAR and still beat random players 92% of the time. I'll concede, though, that it may have been difficult to come across such a player since the presence of a domineering black/white primitive would have hindered the population from "seeing over the trees".

Which brings me to the next factor - the equality of the primitives. As stated before, a single primitive with a potential to output large values relative to its fellow primitives could hinder the population from venturing into a better part of the hypothesis space since the single primitive would overshadow and cause other primitives to become less and less a part of the population, ultimately to the point of extinction.

In part 2, the effect of primitive equality was tested. A simple modification of dividing the black/white values by 8 may have made a difference as the evolved players, both EDGAR-trained and random-trained, demonstrated a noticeable improvement in performance against both random players and EDGAR. And if you notice their GP functions, neither black nor white are used in the evolved players. But it can also be argued that the results could have gone the other way and that the improved results were due only to a more favorable random draw in the population creation and evolution. So, though there is an improvement in the results, the results are only marginally better and not statistically significant enough to come to a definite conclusion.

The next factor - the types of primitives used, played an undisputably larger role in improving the GP othello player. In my primitive set, I introduced a set of primitives that were complete in covering the board, but fewer in number, yet still versatile enough to express any tile on the board. The removal of all redundant primitives, such as the white primitives in this case, also proved to be useful as it further reduced the primitive set, consequently reducing the hypothesis space, which in turn reduced the time of evolution to find a capable player. As the results show, this new set of primitives was definitely more effective as evolved players could beat random players consistently, and when trained against EDGAR, could beat him just as easily as well.

Taking all these factors into account has led to the development of three truly competent othello players in the end. But there is always room for improvement. As can be seen in the final result set, the GP players can still lose against a random player occasionally. And to lose to a random player isn't very impressive. There exists somewhere in a hypothesis space, an othello player that can never lose, but I doubt that the current hypotheses come near to that. In fact, I very much doubt that the current set of primitives is even capable of generating a perfect othello player. There may be an optimal hypothesis within the current space, but I doubt that it could win every game it ever met.

But there are other AI constructs besides genetic programming that could create players. For example, artificial neural nets and search trees could be implemented to create effective othello players as well. And as for a perfect othello player who can play the perfect game, this is indeed possible with the search tree equipped with an infinite search depth and no time restrictions. Unfortunately, even with our current processor speeds, no time restrictions would be unreasonable since the number of branches to search would be astronomical. And so we are still left with the task of coming up with a more perfect othello player using a less exhaustive method, i.e. GPs and ANNs.

So, in conclusion, though much progress has been made through the genetic programming in this project, the search for the perfect othello player continues.