Othello Project

CS W4770 Homework 4, Fall 1997

by Daby Sow

Introduction

The performances of genetic programming schemes are largely due to the representation and fitness measure used. These two entities determine the problem that has to be solved. The representation defines the hypothesis space and the fitness defines what will be understood as a good result. In this work, we have tried to use genetic programming to develop Othello players. We have fixed the representation and have looked for efficient fitness measures. The first section of this document presents an overview of the approach used. Then we present some test results, showing an alternative scheme performing well. We finish with hinting at possible extensions of the proposed method that have the potential to develop better Othello players.

The Approach

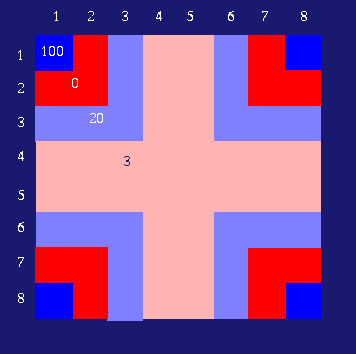
There is no formal way to show that a given fitness measure is better than any other one simply because fitness is just a way for the designer to interact with the computer and tell the machine what "good" means. In other words, the fitness formalizes a notion that can be very subjective. In the provided Othello package, the score of each game is defined by a weighted sum of the length of the hypothesis used and the actual Othello result obtained. While learning how to play Othello against Edgar we realize how important it was to play precisely at certain locations on the board like the corners and how important it was to prevent your opponent from playing at these positions. What we want to show is that the result of the game is more than a direct consequence of the final status of the board and is highly correlated with certain moves at certain locations. That's why we have modified the proposed fitness measure by weighting each moves of the player. Weights are fully defined a priori, by the position of each move as shown in the next figure. The fitness is now equal to the sum on every move of the weights corresponding to the location of the move on the grid. See also OthelloBoard.java for more details.





We decided to assign a different weight to each color of the grid shown above. Blue regions are set to be interesting with a high weight. Red regions are not as interesting because they allow the opponent to move closer the corners in the blue regions. The big red cross at the center of the grid is neutral. Note that the actual result of the game is not used in the computation. Our experiments show that there is a correlation between the result of the game and the fitness that we use. We think that reducing the Othello game to a race to the corners of the board is a simpler task to learn for the computer. The target function can be deducted from the weights on the grid but our genetic players do not have this knowledge. Also, a strategy picking the move with the highest weight may not be optimal simply because there might be many moves with the same weight at any time and choosing the wrong one might prevent the player from reaching a corner in a subsequent move thus reducing its fitness.

Some Experimental Results


All the tests were done against random players. We ran at least 100 games to determine how well our players were doing.


Effects of the Population Size

The parameters used for this part of the work can be found here. The weights of the grid are shown in the next figure:





We were interested on the effects of the size of the population at each generation on the performances and ran some experiments to study this relation. The summary of these experimentations is shown in the next figure.





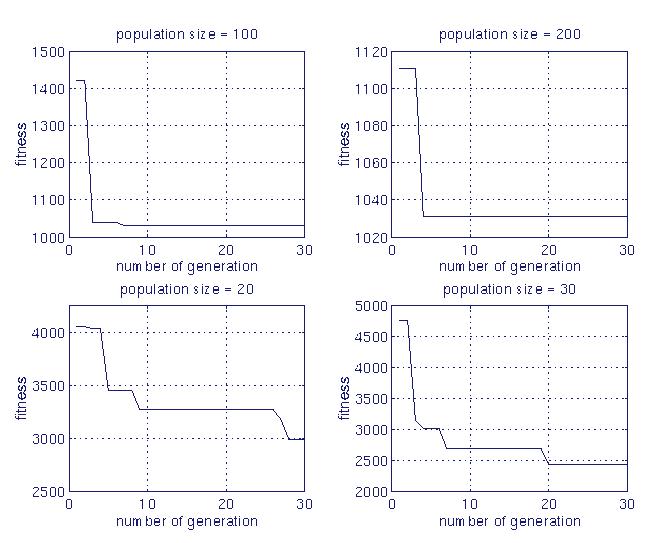
Not surprisingly, we can see that the "time response" (in generations) of the system decreases when the population size increases. More important is the observed fact that the system has an increased ability to converge towards better individual when the size of the population increases. The risks to fall into local minima decreases when the size of the population increases. But the time complexity increases too. This is another variant of the tradeoff between exploration and exploitation. There is also a point after which the system does not improve much. This occurs when the population size is greater than 100. The same individual was identified with runs with population size equal to 100 and 200. The strategy obtained is "white". Its fitness is 1032 on five games when the training was done with a population size of 200. Note that there is a good amount of randomness in the fitness results that we proposed in this report since the training was done against a random player.


Good Individuals

The hypothesis "white" seems to try to minimize the score (number of pieces) of the opponent. This strategy wins only 70% of games played against a random player. To improved this result we have modified the weight grid. We could not find a general rule to adjust these weights (we may need a meta-learning method for that). Nevertheless the system did performed much better by simply changing the 0 weights (red region on the board) to -20. The following individuals were obtained with a population size of 200.




Click here to see how this player was reacting to the moves of the random player.



Click here to see the reaction of this player against the random player.



Click here to see the reaction of this player against the random player.

These individuals are winning slightly less than 95 % of games played against a random player (respectively 93/100 92/100 and 95/100). Their fitnesses are quite low, respectively -190, -129, -172 on five games. We verified that they were actually fighting for the corners of the board. What is interesting here is the fact that using a different fitness measure on an the same hypothesis space can produce good results. It emphasizes the importance of the role of the designer in GP or more generally in machine learning. We cannot expect the system to perform well if the fitness and the function sets do not capture the essence of the problem that has to be solved.


Correlation Between the Fitness and the Game Outcome

In this section we present experimental results showing that the proposed fitness is really correlated to the outcome of the game.





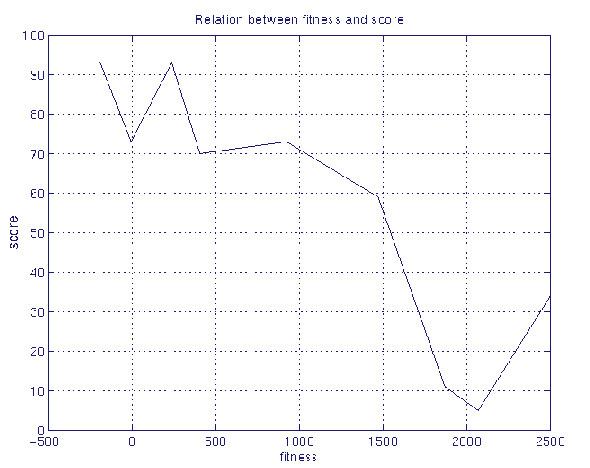
As shown in the graph above, as the fitness increases (the fitness of the opponent), the score, an estimate of the percentage of the number of games won against random players, decreases. there are 9 test points in this plot, coming from 9 different trees. We tried to pick these points uniformly on a fitness interval going from -500 to 2500. There are trees with the same fitness and different scores. A better way to draw this curve would have been to compute the average score for each fitness point using many trees and get a better relation between the score and the fitness. From this plot, we see that the new fitness is not linearly related to the outcome of games but its quasi-monotonic form is an interesting and necessary property for the genetic programming system to perform well.

Concluding Remarks

In this work we saw how an indirect fitness measure can be use to approximate a target function for the Othello game. The indirect fitness measure used has the aspect of a grid weighting each individual moves of the players and we have shown that this fitness is correlated with the number of games won. Several improvements can be made to this approach. First, note that the weight grid has an important effect on the overall performance of the system. We did not try to modify the shape of the different regions. It could be interesting to use a meta-learning technique to adjust these weights. Second, these weights could be updated during the game to better respond to the actions of the opponent. Also, it would be interesting to train and test our players against Edgar and see if there is still an improvement of score when the fitness value increases.


Last update: Dec 12, 1997.