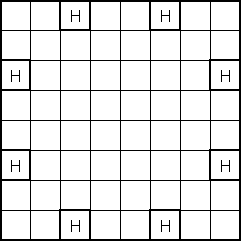
 10 unique positions on board
10 unique positions on board


Chris Porcelli
Patrick Pan
Although we were impressed by the genetic programming package as initially provided, several things needed to be improved. First of all, the set of terminals and operators used, were too coarse to construct a truly good player. Second, playing against random players proved too simple a measure to demonstrate the power of learning capable by a genetic program. To elaborate a bit further on these two points, the program repeatedly arrived (all twenty one times) at the following single node solution: choose the move yielding at the most white pieces next move. This is the strategic ability of a young child.
We wished to create a set of operators and terminals capable of greater expressive power. Or more to the point, capable of representing strategies that my partner and I might come up with rather than a small child.
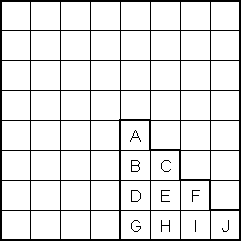
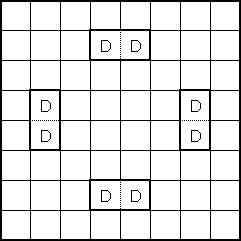
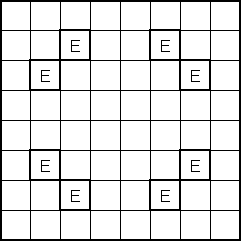
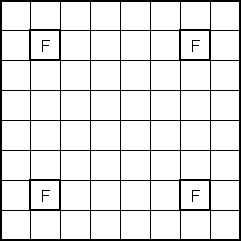
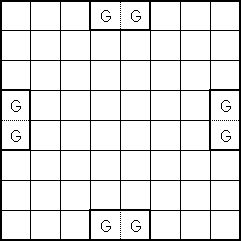
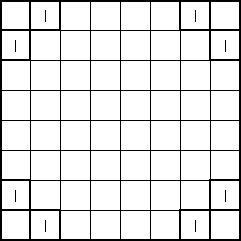
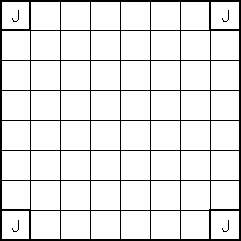
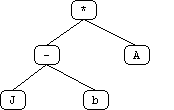
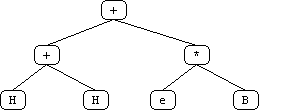
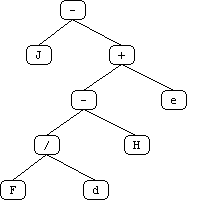
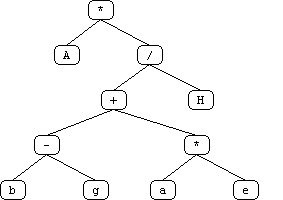
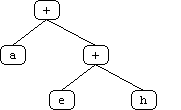
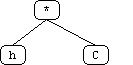
The initial "obvious" solution to this problem is to create a terminal for each position on the board. However, a more sophisticated solution occurred to us after some thought. Utilizing the board's symmetrical properties, we set out to discover the minimum number of "significant" positions representative of all positions on the board. We found ten such positions labeled 'a' through 'j' (see attached diagrams). White piece counts in these positions are in lower case and Black piece counts are in upper case (in the code and genetic program strings, not in the diagrams!).
We modified the initial code to include these new terminals. We also removed the old more general terminals. Our decision to do so, was based largely on the fact that the old terminals could all be expressed by the new set. In addition, the new set was also capable of representing more complex combinations, previously impossible to express. We were aware that leaving the vestigial terminals could have acted as a sort of "compress" operation when equivalent function trees were in competition. However, we decided to remove them due to two factors: the fact that all terminals are passed as arguments to the evaluation functions (increasing the load on the stack) and JAVA's slow performance.
 10 unique positions on board
10 unique positions on board










On attempting to run the GP Othello program on the cs cluster machines, we were met with slow response and computation times. We ran the jobs overnight in an unattended manner using the Unix 'nohup' command due to the nature of the computational task. They were mysteriously deactivated before they could generate the quantity of good runs that were required in the original .ini file. Due to the ubiquitous nature of the Java language and the availability of its interpreters on a variety of computing platforms today, we were able to arrange for the dedication of one of our own team member's (Chris's) machines towards the sole task of continuing our runs and generating Othello players. The transition went fairly smoothly due to the portable nature of Java. In addition, the new machine (A 200-Mhz Pentium) manifested a remarkable improvement in speed and performance in comparison with the original machines it was run on. However, an unforeseen problem had emerged in its wake: while the newly-burdened machine was left unattended with its Protean task of generating satisfactory specimens for the edification of its owners, a nearby rush of power consumption by neighboring residents had resulted in a blackout for the vicinity of those concerned. Whilst my partner had indeed the foresight to install a Universal Power Supply in his residence, the draught of electricity continued for far longer than the life of the temporary servant of energy and the work, which at that time was an accumulation of a night's worth of computation, was lost. Our team pondered this problem and were able to salvage what remained of the experiment. Coding went fairly smoothly on this project, except for the long intermittent period of waiting between runs, and the haphazard chance of something going wrong whenever the computer was left unattended.
The implementation of the changes to the code was tedious but unexpected errors did not arise.
Sample output gifs from our test runs. These were generated with a population of 50 individuals playing against random players. Each individual plays 20 games to score fitness.
What follows are some sample output gifs from our test runs. These were generated with a population of 200 individuals playing against EDGAR. Each individual plays one game to score fitness against him since he always plays the same.

Despite the many complications discussed above, we were pleasantly surprised at the genetic algorithm's ability to learn. It piqued both of our interests, especially in the context of material covered in class, eg., decision trees, neural networks, etc. We were especially surprised at our program's ability to beat Edgar. It appeared that increasing the expressive power of the new terminals resulted in an improvement of performance.
The new factors that were introduced produced a higher sensitivity to the locations of the board. The terminals covered positions on the board that were not considered during play before. This may have lead to an increased sensitivity to all the positions on the board during play. During the training sessions in which our programs trained using Edgar, the genetic player was now able to scrutinize over the entire game board and thus perhaps able to detect patterns in Edgar's occupation of the board and apply this knowledge.
Furthermore, since Edgar seems to exploit the near-corner strategy, our program seemed to gain the advantage in controlling the near-next corner in a game. It appeared to be learning to exploit weaknesses in Edgar's strategy by looking one step beyond what Edgar focused upon. Very little can be learned by playing against a few random players. Almost any strategy can be used to beat a random player, as was demonstrated by the initial package given to us. In addition, playing Edgar only results in strategies that beat Edgar, which makes training difficult since each strategy can play Edgar only once, because Edgar makes the same moves. Which leads us to believe that playing Edgar with a mixture of randomization may be an effective technique.
Or perhaps to utilize the deme concept, with a team of gp's trying to outwit each other. If more time was provided, an extensive study may be feasible. There is a chance that we may propose this topic as a final project.
In addition, intuition suggests that any one step evaluation will always be theoretically inadequate without exploring the entire space and perhaps a better strategy might be to use genetic programs to develop a evaluation function for a heuristic search. The only foreseeable drawback being of course that this will lead to further increasing runtimes, which from our experience is a Bad Thing.
Genetic programming is an effective tool but is limited in its speed. It often requires a long period of time to generate the many different individuals that comprise its search through an ill-understood solution space. During the generation and evaluation, the great expenditure of time for the "evolution" of new "organisms" begins to resemble that of natural forms of evolution (depending on your belief system ;-) ). However, before one concludes that genetic algorithms are pragmatically too slow to have real value, one must remember that they are not theoretically limited in speed. The genetic algorithm is parallelizable by nature and thus their slow performance is largely due to our running them in a sequential manner (and lets not forget in JAVA!). The real theoretical limititation is that research in the field has been mainly empirical and not theoretical. This brings us to our next point.
There is a tradeoff between the exploration of the hypothesis space and the exploitation of the training data. One desires greatly to have two things happen. When a global minima/maxima is encountered we wish our solution to be stable. When a local minima/maxima is encountered we wish our solution to be unstable to allow us to find the global minima/maxima. Clearly these two goals are at odds with each other. There is verly little theoretical analysis on how we ought to deal with balancing this trade off. In addition, the correct balance is highly problem dependant. Which is further at odds with the notion of genetic algorithms being problem independant! Finally, the long execution times make an empirical "tweeking" of the values a long and painful experience.
To illustrate our point concretely, consider the second set of test runs (those against EDGAR). The second to last generated solution hits a local minima at a fitness of 2.03. If you refer the the stc file, you can see that we must wait through 51 generations (at 6 minutes per generation) before the GP realizes this painfully obvious conclusion. We see the flip side of the coin in the last generated solution. In this example, almost by accident, we hit upon a solution that is the best we have ever seen the GP generate, and in only the second generation. Is this the global minima? We can only guess...
Now that we have covered two negative aspects, perhaps we ought now shed the light on one of our more positive observations found conducting our tests on GP's. We were initially concerned that by playing only against Edgar we would be merely learning to beat Edgar, and not developing general strategies for beating other players. However, when we ran several of our strategies that beat Edgar against collections of random players, they all beat the random players over ninety-five percent of the time. This relieved us of our initial fear, but does not conclusively show it to be unfounded.
Ignoring this last qualification, the ways that our program beat Edgar seem to also be applicable to beating the strategies of other human players. When playing Othello, both of us, like Edgar, focused on the squares next to corners. The strategies developed by our GPs often attempt to control the next to near corners. This appears to be both an effective strategy against beating Edgar and also human players.
Hey you got this far...why not take a look at our code...