|
Columbia computer scientists are presenting four papers at FOCS

Columbia theoretical computer scientists are presenting four papers at the 56th Annual IEEE Symposium on Foundations of Computer Science (FOCS) held October 18-20 in Berkeley, CA. One of these papers, An average-case depth hierarchy theorem for Boolean circuits, which solved a problem open for almost 30 years, earned the best paper award. A high-level description of this paper is given below, with abstracts from each of the other papers.
An average-case depth hierarchy theorem for Boolean circuits [Best Paper]
An average-case depth hierarchy theorem for Boolean circuits
Benjamin Rossman, National Institute of Informatics in Japan (to start a professorship at the University of Toronto in 2016) Rocco Servedio, Columbia University Li-Yang Tan, Columbia University, CS PhD'14, now research assistant professor at TTI-Chicago
Are deep Boolean circuits more computationally powerful than shallow ones? If so, by how much? The answers to these questions help computer scientists understand what problems can be solved efficiently by parallel computers.
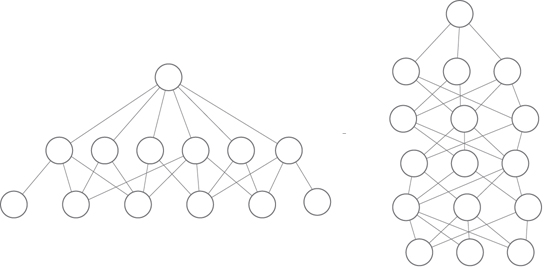
Shallow vs deep: Can a circuit of larger depth (like the depth-6 circuit on the right) efficiently compute functions that a shallower circuit (like the depth-3 circuit on the left) cannot? Each "layer" of circuit depth corresponds to one time step in a parallel computer system, and each node at a given depth corresponds to a processor at that time step.
In a celebrated result from 1986, Johan Håstad proved that shallow circuits can be exponentially less efficient than deeper ones in the worst case. In the language of parallel computation, this means that there are problems that can be solved efficiently in 101 parallel time steps, but to solve them in the worst case (i.e., on every possible input) in only 100 parallel time steps would require exponentially many processors.
For almost 30 years, it has been an open question as to whether what is true in the worst-case—that deep circuits can efficiently compute functions that shallow ones cannot—is also true for the average case.
In An average-case depth hierarchy theorem for Boolean circuits, Benjamin Rossman, Rocco Servedio, and Li-Yang Tan gave an affirmative answer to this question, by proving that for every d, even in the average case, there are functions that are efficiently computable by depth-(d+1) circuits but not by circuits of depth d. Rocco Servedio described the result as follows: "The paper shows that there's a problem that can be solved very efficiently in 101 parallel time steps, i.e., it doesn't require many processors if you get to use that much time. But if you only get 100 rather than 101 parallel time steps, without a really huge number of processors there's no way to do much better than random guessing—for a yes/no question, you won't be able to get the right answer even 51% of the time."
A key technique for the new result is an extension of the "random restriction" method, a classic tool in circuit complexity. This method works by randomly fixing some input variables to constants; the extended method, which the paper calls "random projections," works by additionally identifying certain variables in a carefully designed way (i.e., "projecting" a set of distinct input variables to a common new variable). These variable identifications enable a level of "control" over the random process that makes it possible to prove the lower bound.
The depth hierarchy theorem which is the paper's main result answers several long-standing open questions in structural complexity theory and Boolean function analysis. An average-case depth hierarchy theorem for Boolean circuits received the Best Paper Award at FOCS 2015.
On the Complexity of Optimal Lottery Pricing and Randomized Mechanisms
Xi Chen, Columbia University
Ilias Diakonikolas, School of Informatics, University of Edinburgh Anthi Orfanou, Columbia University Dimitris Paparas, Columbia University Xiaorui Sun, Columbia University Mihalis Yannakakis, Columbia University
The authors of On the Complexity of Optimal Lottery Pricing and Randomized Mechanisms show that even a relatively simple lottery pricing scenario presents a computational problem that one cannot hope to solve efficiently in polynomial time.
In economics, lottery pricing is a strategy for maximizing a seller's expected revenue. Unlike item pricing, the seller does not fix the price of each item but offers the buyer lotteries at different prices (according to a probability distribution). For example, the seller may offer the buyer, at a certain price, 50% chance of getting item 1 and 50% chance of getting item 2. Lotteries create for the seller a bigger space to price things, and lottery pricing has been shown in some cases to achieve strictly higher revenues for the seller than the seller can get from item pricing.
The computational problem for the seller is to figure out an optimal menu (or set) of lotteries that maximizes the seller's revenue, and the authors consider the case when there is a single unit-demand buyer. This setup is similar to the optimal item pricing problem that the authors examined last year in another paper.
Moving from item pricing to lottery pricing, however, completely changes the computational problem. While item pricing is in some ways a discrete problem, lottery pricing is essentially continuous given its linear program characterization that involves exponentially many variables and constraints. Though it had been previously conjectured that the optimal lottery pricing problem is hard, it required a delicate construction and a 30-page proof from the authors to finally obtain the hardness evidence.
That evidence is summarized in On the Complexity of Optimal Lottery Pricing and Randomized Mechanisms, where the authors show that even for a simple lottery scenario—one seller and one unit-demand buyer—it's not possible to solve the pricing problem efficiently in polynomial time without adding in conditions or special cases. Via a folklore connection, the result also provides the same hardness evidence for the problem of optimal mechanism design under the same simple setup.
Indistinguishability Obfuscation from the Multilinear Subgroup Elimination Assumption
Indistinguishability Obfuscation from the Multilinear Subgroup Elimination Assumption
Craig Gentry, IBM T.J. Watson Research Center, Allison Lewko Bishop, Columbia University, Amit Sahai, University of California at Los Angeles Brent Waters, University of Texas at Austin
Abstract:
We revisit the question of constructing secure general-purpose indistinguishability obfuscation, with a security reduction based on explicit computational assumptions over multilinear maps. Previous to our work, such reductions were only known to exist based on meta-assumptions and/or ad-hoc assumptions: In the original constructive work of Garg et al. (FOCS 2013), the underlying explicit computational assumption encapsulated an exponential family of assumptions for each pair of circuits to be obfuscated. In the more recent work of Pass et al. (Crypto 2014), the underlying assumption is a meta-assumption that also encapsulates an exponential family of assumptions, and this meta-assumption is invoked in a manner that captures the specific pair of circuits to be obfuscated. The assumptions underlying both these works substantially capture (either explicitly or implicitly) the actual structure of the obfuscation mechanism itself.
In our work, we provide the first construction of general-purpose indistinguishability obfuscation proven secure via a reduction to a natural computational assumption over multilinear maps, namely, the Multilinear Subgroup Elimination Assumption. This assumption does not depend on the circuits to be obfuscated (except for its size), and does not correspond to the underlying structure of our obfuscator. The technical heart of our paper is our reduction, which gives a new way to argue about the security of indistinguishability obfuscation.
Robust Traceability from Trace Amounts
Cynthia Dwork, Microsoft Research
Adam D. Smith, Pennsylvania State University Thomas Steinke, Harvard University Jonathan Ullman , Columbia University CS PhD'14, now assistant professor at Northeastern University
Abstract.
In 2008, Homer et al. (PLoS Genetics) demonstrated the privacy risks inherent in the release of a large number of summary statistics (specifically, 1-way marginals of SNP allele frequencies) about participants in a genome-wide association study. Specifically, they showed how given a large number of summary statistics from a case group (a dataset of individuals that have been diagnosed with a particular disease), the data of a single target individual, and statistics from a sizable reference dataset independently drawn from the same population, they could determine with confidence whether or not the target is in the case group. That is, the trace amount of data (DNA) that the target individual contributes to the summary statistics enables his or her presence in the case group to be traced by an adversary. The Homer et al. work had a major impact, changing the way that the US NIH and Wellcome Trust allow access to information from studies they fund.
In this work, we describe and analyze a simple attack that works even if the summary statistics are distorted significantly, whether due to measurement error or noise intentionally introduced to protect privacy (as in differential privacy). Our attack only requires that bias of the statistics are bounded by a small additive constant on average (i.e., the expectation of the vector of summary statistics is close to the vector of true marginals in ℓ1 norm). The reference pool required by previous analyses is replaced by a single sample drawn from the underlying population. The attack is not specific to genomics.
The new attacks work by significantly generalizing recent lower bounds for differential privacy based on fingerprinting codes (Bun, Ullman, and Vadhan, STOC 2014; Steinke and Ullman, 2015). The attacks implicit in those works assume that the attacker controls the exact distribution of the data. Our analysis allows for tracing even when the attacker has no knowledge of the data distribution and only a single reference sample, and also works for real-valued (Gaussian) data in addition to discrete (Bernoulli) data.
Posted 10/19/2015
|