

Next: Applications
Up: Modelling Trajectory as a
Previous: Linear Motion
Let O be a set of 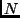 points on the planar trajectory of a point
and let
points on the planar trajectory of a point
and let 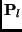 be its images using an affine camera in view
be its images using an affine camera in view 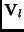 , where
, where 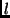 is the view index. Let
is the view index. Let
![$(u^l[i], v^l[i])$](img77.png) be the image
coordinates of points on the contour traced out in view
be the image
coordinates of points on the contour traced out in view 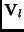 . We
represent this contour using a sequence of vectors of complex numbers as
given below.
. We
represent this contour using a sequence of vectors of complex numbers as
given below.
Under affine projection, the image-to-image homography between a pair of
views is affine also. Thus, the corresponding points of the contour in
view 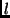 are related to the points in the reference view
are related to the points in the reference view 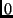 by the
relation
by the
relation
![\begin{displaymath}{\bf x}^l[i] = {\bf A}_l {\bf x}^0[i] + {\bf b_l},
\;\; 0 \leq i < N
\end{displaymath}](img80.png) |
(15) |
where 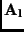 is an arbitrary
is an arbitrary 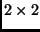 matrix. Taking the Fourier
transform of Equation 15, we get
matrix. Taking the Fourier
transform of Equation 15, we get
which can be rewritten as (ignoring the DC component k = 0)
![\begin{displaymath}
{\bf X}^l[k] = {\bf A_l} {\bf X}^0[k],\;\; 0 < k < N
\end{displaymath}](img84.png) |
(16) |
where
![${\bf X}^l = \left[{\bf U}^l,\;\; {\bf V}^l\right]^{\sc T}$](img85.png) ;
;
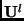 and
and 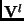 are Fourier transform sequences of
are Fourier transform sequences of 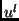 and
and
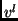 respectively. We can now define the following measure
respectively. We can now define the following measure 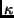 for
the points on the contour in the view
for
the points on the contour in the view 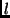 as
as
![\begin{displaymath}
\kappa^l[k] = ({\bf {X}}^l[k])^{*{\sc T}}
\left[ \begin{arr...
...1\;\; & 0 \end{array} \right] {\bf\bar{X}}^l[k],\;\; 0 < k < N
\end{displaymath}](img91.png) |
(17) |
(* denotes the complex conjugate). It can be shown that [10]
![\begin{displaymath}
\kappa^l[k] = \vert{\bf A_l}\vert\; \kappa^0[k],\;\; 0 < k < N.
\end{displaymath}](img92.png) |
(18) |
where, 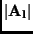 denotes the determinant of
denotes the determinant of 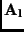 .
The
.
The 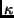 values defined by Equation 17, which can be
computed independently for each view from the Fourier transform of the
contour points, identify the contour formed by the motion, upto
a scale factor. Consider the following
values defined by Equation 17, which can be
computed independently for each view from the Fourier transform of the
contour points, identify the contour formed by the motion, upto
a scale factor. Consider the following 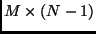 matrix for
matrix for 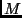 views of the planar contour
views of the planar contour
![\begin{displaymath}
\Theta =
\left[ \begin{array}{cccc}
\kappa^0[1] & \kappa^...
...1] & \cdots & \cdots & \kappa^{M-1}[N-1]
\end{array} \right].
\end{displaymath}](img96.png) |
(19) |
It can be seen from Equation 18 that rank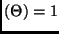 .
See reference [10] for a detailed discussion on rank constraints for
shape matching.
.
See reference [10] for a detailed discussion on rank constraints for
shape matching.
Equation 19 gives a constraint on measures that can be
computed from each view independently. The trajectory of a point moving
in a plane can be tracked over time to generate the contour in each view.
This constraint is view and time independent. There are no restrictions
on the number of views or frames per se. In practice, however, the
Fourier transform will be reliable only if the curve has sufficient
length. The motion of the point is arbitrary. If a number of points can
be tracked independently, each contour will yield a different constraint,
all of which have to be satisfied simultaneously. It is clear that
non-rigid motion is also covered by these constraints.


Next: Applications
Up: Modelling Trajectory as a
Previous: Linear Motion
2002-10-10
![]() points on the planar trajectory of a point
and let
points on the planar trajectory of a point
and let ![]() be its images using an affine camera in view
be its images using an affine camera in view ![]() , where
, where ![]() is the view index. Let
is the view index. Let
![]() be the image
coordinates of points on the contour traced out in view
be the image
coordinates of points on the contour traced out in view ![]() . We
represent this contour using a sequence of vectors of complex numbers as
given below.
. We
represent this contour using a sequence of vectors of complex numbers as
given below.