

Next: Discussion on Multiview Relations
Up: Algebraic Constraints on Moving
Previous: View Consistency
We take a look at how the above relationships can be extended to
perspective cameras. Suppose that we have a world point 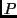 that moves
as per Equation 1. Let this point be viewed by
a perspective camera represented by the camera matrix
that moves
as per Equation 1. Let this point be viewed by
a perspective camera represented by the camera matrix 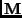 . The
projection of
. The
projection of 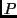 will trace a line in the image. Let us represent this
line
will trace a line in the image. Let us represent this
line 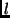 by
by
![\( \left [ \begin{array}{ccc} a & b & c \end{array}\right]^{\sc T}.\)](img126.png) Let
Let 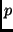 be the projection of
be the projection of 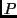 due to
due to 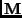 at
some time instant
at
some time instant 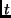 .
.
Differentiating w.r.t. 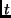 , we get
, we get
Proceeding in a similar manner as before to eliminate the projection
terms 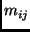 , we can derive a view-independent relation for uniform
velocity motion under perspective projection. However, the number of
unknowns are very high and hence the number of views or time instants
needed to solve for them runs into a large number. Extension to constant
acceleration motion also has similar properties under perspective
projection. Levin et al. sketch the extension of their view-independent
constraints to perspective cameras. Their extension required 6 points in
49 time instants under perspective projection, compared to 5 points in 8
time instants under affine projection. Similar ideas must be applied to
reduce the view requirements to practical levels. We are actively
pursuing this currently.
, we can derive a view-independent relation for uniform
velocity motion under perspective projection. However, the number of
unknowns are very high and hence the number of views or time instants
needed to solve for them runs into a large number. Extension to constant
acceleration motion also has similar properties under perspective
projection. Levin et al. sketch the extension of their view-independent
constraints to perspective cameras. Their extension required 6 points in
49 time instants under perspective projection, compared to 5 points in 8
time instants under affine projection. Similar ideas must be applied to
reduce the view requirements to practical levels. We are actively
pursuing this currently.


Next: Discussion on Multiview Relations
Up: Algebraic Constraints on Moving
Previous: View Consistency
2002-10-10
![]() that moves
as per Equation 1. Let this point be viewed by
a perspective camera represented by the camera matrix
that moves
as per Equation 1. Let this point be viewed by
a perspective camera represented by the camera matrix ![]() . The
projection of
. The
projection of ![]() will trace a line in the image. Let us represent this
line
will trace a line in the image. Let us represent this
line ![]() by
by
![]() Let
Let ![]() be the projection of
be the projection of ![]() due to
due to ![]() at
some time instant
at
some time instant ![]() .
.