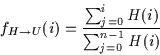 |
(4.20) |
![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) and Equation
and Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) depict the
mapping to a uniform distribution which is also known as histogram
equalization [14]:
depict the
mapping to a uniform distribution which is also known as histogram
equalization [14]:
where n is the number of discrete intensity levels, for 8-bit images, n=256.
To find the mapping function,
![]() ,
we invert the function
,
we invert the function
![]() to obtain
to obtain
![]() .
Since the domain and the range of the
functions of this form are identical, the inverse mapping is trivial and is
found by cycling through all values of the function. However, due to the
discrete nature of these functions, inverting can yield a function which is
undefined for certain values. Thus, we use linear interpolation and assume
smoothness to fill undefined points of the inverse function according to the
values of well-defined points in the function. Thus, we generate a fully
defined mapping
.
Since the domain and the range of the
functions of this form are identical, the inverse mapping is trivial and is
found by cycling through all values of the function. However, due to the
discrete nature of these functions, inverting can yield a function which is
undefined for certain values. Thus, we use linear interpolation and assume
smoothness to fill undefined points of the inverse function according to the
values of well-defined points in the function. Thus, we generate a fully
defined mapping
![]() which transforms a uniform histogram
distribution to the distribution found in histogram G(i). The mapping
which transforms a uniform histogram
distribution to the distribution found in histogram G(i). The mapping
![]() can then be defined as in Equation
can then be defined as in Equation ![[*]](http://vismod.www.media.mit.edu/vismod/support/latex2html-98//cross_ref_motif.gif) :
: