Semi-Elliptical Sampling Regions

The sampling regions for the real-time symmetry transform are circular concentric rings of varying size and thickness (see Figure ). The use of circular rings is ideal for detecting rotational invariance. However, we wish to develop an operator which will detects blobs of a certain form. This requires specific annular sampling regions to detect the contours of interest in the image. In other words, the sampling region should approximate the shapes we are searching for in the image. We proceed by defining a parameterized mathematical model of the templates to approximate facial contours. Figure  depicts the geometry of this so-called semi-elliptical model. It is a superset of the class of elliptical annuli which is itself a superset of the class of circular annuli. Such a model lends itself quite well to detecting human face and head contours which are not well-approximated by simple ellipses or circles. The model can be viewed as two half ellipses spliced together along a shared axis of length b. The model has the following parameters:

a

Length of one elliptical axis

b

Length of shared elliptical axis

c

Length of another elliptical axis

$\phi$

Orientation of model with respect to vertical

t

Thickness as a scale factor of the model

  

Figure 2.13: The semi-elliptical model

If a=c the model becomes an elliptical sampling region; if a=b=cthe template models a circular sampling region.

By varying the parameters of the model, we can generate the desired blob templates. The orientations of the normals at the boundary of the template are also pre-computed by a template generation process. Note that the orientation of the normals varies not only as a function of the angular position on the sampling region but also as a function of the radius from the center. The center of the model is a well defined point: it is the intersection of the shared elliptical axis and the meeting point of the other two axes (a and c).

The equations for an for an ellipse's boundary and its contour's normals are used to construct the templates [43]:

$$r=\frac{ab}{\sqrt{a^{2}\cos(\theta)^{2}+b^{2}\sin(\theta)^{2}}}$$ (2.6)

$$\rho=\arctan(\frac{2r(b^{2}\sin(\theta)^{2}+a^{2}\cos(\theta)... ...^ {\frac{3}{2}}}{ab(a^{2}-b^{2})\sin(2\theta)})-\frac{\pi}{2}$$ (2.7)

a

length of major axis ( a₁<a<a₂)

b

length of minor axis ( b₁<b<b₂)

$\theta$

angle of ellipse minor axis with respect to vertical

r

radius

$\rho$

angle between radius vector and boundary normal

Figure  depicts a typical template consisting of a semi-circular annulus on top of a semi-elliptical annulus. The orientation values of the normals of the template are represented by intensity. Note the similarity of this template to the shape of a human head or face.

  

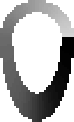Figure 2.14: A sample template for face or head-like blob detection with template normals represented with intensity