



Next: Machine Learning: Practical Considerations
Up: Action-Reaction Learning: Analysis and
Previous: Probabilistic Time Series Modeling
Beyond EM: Generalized Bound Maximization,
Conditional Densities and the CEM Algorithm
-
- In the following chapters, we present a section dedicated to the
machine learning aspect of this work. The concept of learning and
probabilistic estimation is central to the Action-Reaction Learning
paradigm and framework. The objective is to learn a mapping between
the past interaction (
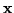 )
and the most likely reaction (
)
and the most likely reaction (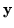 )
of humans from video data. This machine learning problem requires
special attention and we describe a novel approach to resolving
it. The contribution here is to stress that Action-Reaction Learning
is best considered as a discriminatory learning problem and we show a
formal Bayesian description of it. Essentially, we would like to
estimate and use a conditional probability,
)
of humans from video data. This machine learning problem requires
special attention and we describe a novel approach to resolving
it. The contribution here is to stress that Action-Reaction Learning
is best considered as a discriminatory learning problem and we show a
formal Bayesian description of it. Essentially, we would like to
estimate and use a conditional probability,
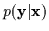 .
However, traditional tools such as the EM (Expectation
Maximization) [15] algorithm do not apply. Therefore, we
instead propose an optimization framework and derive the CEM
(Conditional Expectation Maximization) algorithm to resolve the
problem.
.
However, traditional tools such as the EM (Expectation
Maximization) [15] algorithm do not apply. Therefore, we
instead propose an optimization framework and derive the CEM
(Conditional Expectation Maximization) algorithm to resolve the
problem.
-
- We discuss important differences between conditional density
estimation and conditioned joint density estimation in practical
machine learning systems and at a Bayesian level. This motivates the
use of direct conditional estimation and maximum conditional
likelihood. To this end, we introduce and argue favorably for the
generalized bound maximization (GBM) framework. The approach
encompasses a variety of bounding methods that are useful for many
optimization and learning problems. In particular, we apply these
techniques to develop the Conditional Expectation Maximization (CEM)
algorithm which maximizes conditional likelihood. The GBM techniques
extend the bounds computed by the EM algorithm and offer reliable
optimization and convergence. In addition, the bounding techniques are
more general and can be applied to functions which can not be posed as
maximum-likelihood incomplete-data problems. Essentially, we
reformulate gradient ascent steps as optimization of a bound and avoid
ad hoc estimation of step size. The approach is guaranteed to maximize
the given function at each step and local convergence is
proven. Unlike gradient techniques, the GBM framework is amenable to
deterministic annealing and can be used to search for global optima. Results
are shown for conditional density estimation as well as nonlinear
function optimization.




Next: Machine Learning: Practical Considerations
Up: Action-Reaction Learning: Analysis and
Previous: Probabilistic Time Series Modeling
Tony Jebara
1999-09-15