Since the video camera is aligned with the line of sight, by gazing at interesting objects, the user directs the input to the recognition system which tries to recognize previously recorded objects. The recognition results are then sent to the audio-visual associative memory system which plays the appropriate clip.
The generic object recognition system used by DyPERS has been recently proposed by Schiele and Crowley [Schiele and Crowley, 1996]. A major result of their work is that a statistical representation based on local object descriptors provides a reliable means for the representation and recognition of object appearances.
Objects are represented by
multidimensional histograms of vector responses from local
neighborhood operators. Simple matching of
such histograms (using ![]() -statistics or intersection
[Schiele and Crowley, 1997])
can be used to determine the most probable object, independent of its
position, scale and image-plane rotation. Furthermore the approach is
considerably robust to view point changes. This technique has been
extended to probabilistic object recognition [Schiele and Crowley, 1996], in
order to determine the probability of each object in an image only
based on a small image region. Experiments (briefly described below)
showed that only a small portion of the image (between 15% and
30%) is needed in order to recognize 100 objects correctly. In the
following we summarize the probabilistic object recognition technique
used. The current system runs at approximately 10Hz on a Silicon
Graphics O2 machine using OpenGL extensions for real-time image
convolution.
-statistics or intersection
[Schiele and Crowley, 1997])
can be used to determine the most probable object, independent of its
position, scale and image-plane rotation. Furthermore the approach is
considerably robust to view point changes. This technique has been
extended to probabilistic object recognition [Schiele and Crowley, 1996], in
order to determine the probability of each object in an image only
based on a small image region. Experiments (briefly described below)
showed that only a small portion of the image (between 15% and
30%) is needed in order to recognize 100 objects correctly. In the
following we summarize the probabilistic object recognition technique
used. The current system runs at approximately 10Hz on a Silicon
Graphics O2 machine using OpenGL extensions for real-time image
convolution.
Multidimensional receptive field histograms are constructed using a vector of any linear filter. Due to the generality and robustness of Gaussian derivatives, we selected multidimensional vectors of Gaussian derivatives (typically the magnitude of the first derivative and the Laplace operator at two or three different scales). In order to recognize an object, we are interested in computing the probability of the object On given a certain local measurement Mk (here a multidimensional vector of Gaussian derivatives). This probability p(On|Mk) can be calculated using Bayes rule:
Having K independent local measurements M1, M2, ![]() MKwe can calculate the probability of each object On by:
MKwe can calculate the probability of each object On by:
Mk corresponds to a single
multidimensional receptive field vector. Therefore K local
measurements Mk correspond to K receptive field vectors which are
typically from the same region of the image. To guarantee
independence of the different local measurements we choose the
minimal distance
d(Mk,Ml) between two measurements Mk and Ml
to be sufficiently large (in the experiments below we chose the
minimal distance
![]() ).
).
In the following we assume the a priori probabilities p(On) to be
known and use
![]() for the calculation
of the a priori probability p(Mk). Since the probabilities
p(Mk|On) are directly given by the multidimensional receptive
field histograms, Equation
(1) shows a calculation of the
probability for each object On based on the multidimensional
receptive field histograms of the N objects. Perhaps the most
tempting property of Equation (1) is that we do not need
correspondence. That means that the probability can be calculated for
arbitrary points in the image. Furthermore the complexity is linear in
the number of image points used.
for the calculation
of the a priori probability p(Mk). Since the probabilities
p(Mk|On) are directly given by the multidimensional receptive
field histograms, Equation
(1) shows a calculation of the
probability for each object On based on the multidimensional
receptive field histograms of the N objects. Perhaps the most
tempting property of Equation (1) is that we do not need
correspondence. That means that the probability can be calculated for
arbitrary points in the image. Furthermore the complexity is linear in
the number of image points used.
 |
Equation (1) has been applied to a
database of 103 objects. In an experiment 1327 test images of the 103
objects have been used which include scale changes up to ![]() %,
arbitrary image plane rotation and view point changes. Figure
4 shows results which were obtained for
six-dimensional histograms, e.g. for the filter combination
Dx-Dy-Lap at two different scales (
%,
arbitrary image plane rotation and view point changes. Figure
4 shows results which were obtained for
six-dimensional histograms, e.g. for the filter combination
Dx-Dy-Lap at two different scales (
![]() and = 4.0). A
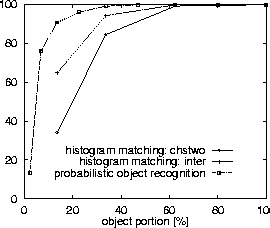
visible object portion of approximately 62% is sufficient for the
recognition of all 1327 test images (the same result is provided by
histogram matching). With 33.6% visibility the recognition rate is
still above 99% (10 errors in total). Using 13.5% of the object the
recognition rate is still above 90%. More remarkably, the recognition
rate is 76% with only 6.8% visibility of the object. See
[Schiele and Crowley, 1996,Schiele and Crowley, 1997] for further details.
and = 4.0). A
visible object portion of approximately 62% is sufficient for the
recognition of all 1327 test images (the same result is provided by
histogram matching). With 33.6% visibility the recognition rate is
still above 99% (10 errors in total). Using 13.5% of the object the
recognition rate is still above 90%. More remarkably, the recognition
rate is 76% with only 6.8% visibility of the object. See
[Schiele and Crowley, 1996,Schiele and Crowley, 1997] for further details.