Frequency Domain Normal Map Filtering

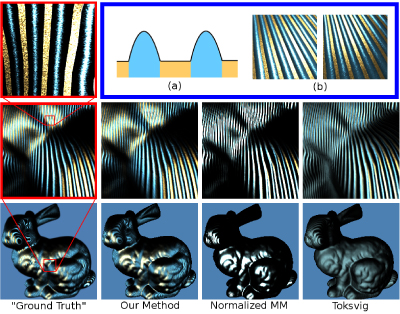
Charles Han Bo Sun Ravi Ramamoorthi Eitan Grinspun

Columbia University

Abstract

Filtering is critical for representing image-based detail, such as textures or normal maps, across a variety of scales. While mipmapping textures is commonplace, accurate normal map filtering remains a challenging problem because of nonlinearities in shading--we cannot simply average nearby surface normals. In this paper, we show analytically that normal map filtering can be formalized as a spherical convolution of the normal distribution function (NDF) and the BRDF, for a large class of common BRDFs such as Lambertian, microfacet and factored measurements. This theoretical result explains many previous filtering techniques as special cases, and leads to a generalization to a broader class of measured and analytic BRDFs. Our practical algorithms leverage a significant body of previous work that has studied lighting-BRDF convolution. We show how spherical harmonics can be used to filter the NDF for Lambertian and low-frequency specular BRDFs, while spherical von Mises-Fisher distributions can be used for high-frequency materials.

Files

Paper:: [PDF]
Video:: [AVI, 103MB]
Trailer:: [MOV, 53MB]
Slides:: [PPT]
Example GLSL Code:: [Spherical Harmonics vertex shader] [Spherical Harmonics fragment shader] [vMF vertex shader] [vMF fragment shader]

BibTeX

@article{HSRG07,
    author = {Charles Han and Bo Sun and Ravi Ramamoorthi and Eitan Grinspun},
    title = {Frequency Domain Normal Map Filtering},
    journal = {ACM Transactions on Graphics (Proceedings of SIGGRAPH 2007)},
    year = {2007},
    volume = {26},
    number = {3},
    pages = {28:1--28:12}
}