A Theory of Frequency Domain Invariants: Spherical Harmonic Identities for BRDF/Lighting Transfer and Image Consistency
Dhruv Mahajan Ravi Ramamoorthi Brian Curless
Columbia University Columbia University University Of Washington

Fig. 1
This work develops a theory of frequency domain invariants in computer vision. We derive novel identities using spherical harmonics, which are the angular frequency domain analog to common spatial domain invariants such as reflectance ratios. These invariants are derived from the spherical harmonic convolution framework for reflection from a curved surface. Our identities apply in a number of canonical cases, including single and multiple images of objects under the same and different lighting conditions. One important case we consider is two different glossy objects in two different lighting environments. For this case, we derive a novel identity, independent of the specific lighting configurations or BRDFs, that allows us to directly estimate the fourth image if the other three are available (Fig. 1,2). The identity can also be used as an invariant to detect tampering in the images (Fig. 2). We also adapt Wiener filtering from image processing, deriving the deconvolution filters to estimate complex lighting from the single image of an object (Fig. 3).
While this paper is primarily theoretical, it has the potential to lay the mathematical foundations for two important practical applications. First, we can develop more general algorithms for inverse rendering problems, which can directly relight and change material properties by transferring the BRDF or lighting from another object or illumination (Fig. 1,2). Second, we can check the consistency of an image, to detect tampering or image splicing (Fig. 2).
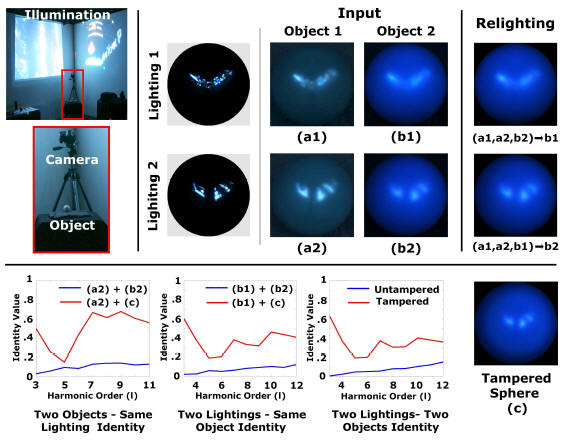
Fig. 2
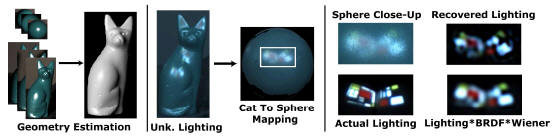
Fig. 3
PAMI Paper: [PDF]
ECCV 2006 Paper: [PDF]