Problem:

Implement an R-Tree index for 2-dimensional points. For simplicity, we will assume that the R-tree will be static, and the only operation is bulk loading. For searching, the R-Tree index should support point and range queries. Finally, the index should also support special functionality to find the data points that maximize a given linear function efficiently.

bulk loading:

Map each 2-dimensional data point (x1, x2) to its 1-dimensional Hilbert value by calling function getHilbertValue(x1, x2).

unsigned long getHilbertValue(int x1, int x2) {
  unsigned long res = 0;
  int BITS_PER_DIM = 16;
  for (int ix = BITS_PER_DIM; ix >= 0; ix--) {
    unsigned long h = 0;
    unsigned long b1 = (x1 & (1 << ix)) >> ix;
    unsigned long b2 = (x2 & (1 << ix)) >> ix;


    if (b1 == 0 && b2 == 0) {
    h = 0;
    } else if (b1 == 0 && b2 == 1) {
    h = 1;
    } else if (b1 == 1 && b2 == 0) {
    h = 3;
    } else if (b1 == 1 && b2 == 1) {
    h = 2;
    }
    res += h << (2 * ix);
  }
  return res;
}

Algorithm: (This algo was developed by myself long time ago ^_^ )

Maximization:

Given two positive integers a1 and a2, you should return all the points among the indexed data set that maximize the linear function f(x1, x2)=a1 x1 + a2 x2 in the data set. For example, if the indexed set of data points is {(8, 1), (7, 2), (3, 5)}, with a1=1 and a2=2, then the answer should be point (3, 5), since f(3, 5)=1*3 + 2*5=13 is larger than f(8, 1)=10 and f(7, 2)=11. In contrast, for a1=a2=1, the answer should be points (8, 1) and (7, 2), since f(8, 1)=f(7, 2)=9, which is larger than f(3, 5)=8.

Algorithm:

The value of x1 and y1 are between 0 and 65536. So draw a diagram like this:

Then pick up a point arbitrarily say A and draw a horizontal line and a vertical line cross A.

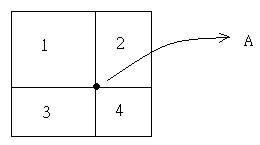
The maximization value of any point in area 3 is smaller then area 2. But we don't sure the value in 1 and 4. To test the maximization value, we only need to test the points in area 1, 2 and 4. We can get these points by range query. Therefore, if we can make area 3 vary large and others very small, we only need to check a few points.(see below) This is the basic idea.

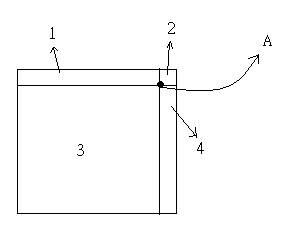
So, how to choose A? Assume we don't know anything. We pick up the most reasonable point, the mid point.

The first A that we pickup is (65536/2, 65536/2) = (32768, 32768).

Next, we test whether there is any point in area 2 or not.

Step 1:

If it doesn’t have any point, we pick up the next mid point in area 3, (32768-32768/2, 32768-32768/2), pick up the next mid point in area 3, pick up the next mid point in area 3…….. Until we find that there is any point in the area we are checking, go to step 2.

If the area we are checking is too small, but it’s still empty, we stop, too. This situation means all of the points are in a small area and close to (0, 0). This is a special case. For example, all of the x value or y value of points are smaller than 2. Then I will scan the whole data. This would not happen in our case.

Step 2:

If it does have points in area 2, we pick up the next mid point in area 2, which is (32768+32768/2, 38768+38768/2). Until we find there is no point in the area we are checking, we stop. And get the previous checking point (previous A). Go to step 3.

Step 1 and 2 are a kind of "bisection checking". The cost is small. Because in each "check", we call range query but don't need to get all of the points in that area. When we get the first point, we stop, and return "true". We only have to know whether the area has points or not. We don't care about how many points there or what the points are. So, the cost of each step is the height of the R-tree. If, C = 10, D = 10 in our case, it’s only 5. If we run 10 times, area 2 will become a 32x32 square, which is very small in a 65536x65536 area. And the cost now is just 10*5 = 50.

Step 3:

Now, our checking point (A) is very close to the up-right corner, and area 2 does have points. There are only a few points in area 1, 2 and 4.

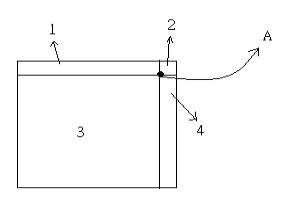
            However, we can make a closer guess. See this picture:

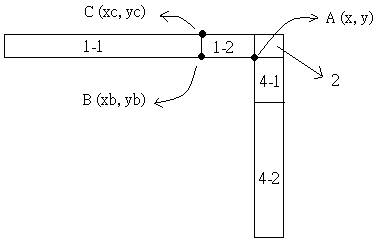
We don't need points in area 1-1, and the coordinates of B is (xb, yb), C is

(xc, yc) yb = y, yc = 65536 and xb = xc = x - ((65536-y)*a2)/a1.

Proof:

0.      "The smallest point" means the point which has the smallest maximization   

      value. "The biggest point" means the point which has the biggest 

      maximization value.

1.      The smallest point in area 2 is A(x, y).

2.      If a point in area 1 is bigger than points in area 2, it must have a very big y.

3.      The biggest y is 65536.

4.      The biggest point in area 1-1 and is smaller than A has the same y value of yc and its x value is smaller than xc which is C

5.      F1(x) = a1*x1 + a2*y1 = F2(x) = a1*x2 + a2*y2

6.      For point A and point C: a1*x + a2*y = a1*xc + a2*yc,   yc = 65536

7.      a1*xc = a1*x – ((a2*yc)-a2*y) è xc = x - ((65536-y)*a2)/a1

We can get 4-1 and 4-2 by the same way.

Step 4:

            Now, we call range query for this area:

(rectangle a, c, f, d and rectangle e, f, h, g)

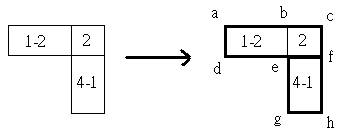
            Then check the maximization value for the points.