Orthogonality Tutorial

Thou art Orthogonal

The power of linear algebra is in visualizing the vectors so that we may exploit the physical geometry of the system to immediately get the answer. Orthogonality () is a highlight of this principle. So many important concepts (e.g., "closeness", "unrelatedness", etc.) are associated with this abstract notion, making it extremely useful as well as beautiful.

A prototypical illustration of orthogonality is the Least Squares Approximations (LSA). I never liked that name. It comes up often, but what does that even mean? Sounds complicated! Strang's textbook gives an excellent presentation on LSA, but I'll try to make it more fun and intuitive.

LSA: Reach for the Unreachable Solution

Let's get the obvious question out of the way. What does that name LSA mean? In its full version, it stands for "Using the orthogonality of vectors to give Least Squared length of the error vector in your Approximations of the solution".

Why do we even need to resort to approximations? Suppose you want to find a linear function f (in real) that satisfies certain conditions. You might say, "It can be whatever, but I want it to spit out 0 on 0 and 1.1 on 1.1". In this case, there is a unique f that grants your wish, namely f(x) = x.

But in reality, you are more picky. If you want a linear f to spit out 0 on 0, 1.1 on 1.1 and 2 on 1.5, tough luck; there is no such f, becaue you cannot spear three points with a line if they're not on it.
To see precisely why we have no solution, we turn to linear algebra. The task is to model f under input-output constraints (x_1,y_1)...(x_n,y_n). Any f(x) can be expressed as B + S * x, a line defined by the input x, bias B, and slope S. Thus, the bottom line is we want to find some values for B and S such that the following is satisfied.
First Leap: Realize that this system can be written in matrix multiplication
.

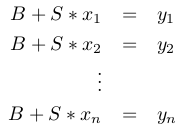
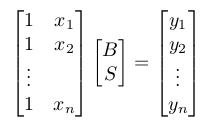This is just Ax=b if we define .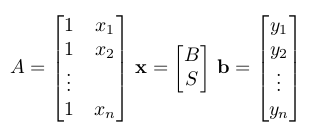

Let's look at A, which is an nx2 matrix. The rank (:= the number of "pivots", or the head of nonzero rows after forward elimination) of A is going to be at most 2. The Fundamental Theorem of Linear Algebra then tells us that the space spanned by the two columns of A can have dimension at most 2. If we were to have an exact solution for x, b must be in this column space, but it is unlikely that b will be in such a small space if n > 2. (Of course, the best scenario is A is square and invertible so that we can simply compute , but that's out of question as soon as you have more than two equations to satisfy.)

Now that we know we don't have an exact solution, no matter what B and S we pick for x, Ax is not going to be equal to b and consequently the error e = b - Ax is going to be nonzero. How do we make the error as small as possible? This is where visualizing vectors is useful.

Projection: Follow the Shadow

Ordinarily, when we have two vectors v and w, we want to somehow relate them. A good way is to "project" one (say v) onto the other, and examine the "shadow" p of v on w.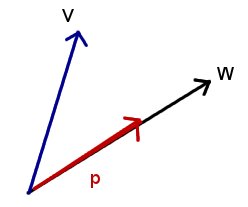
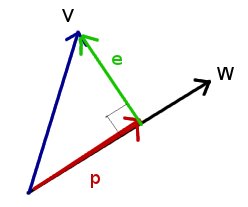
How do we find such projection? Second Leap: v decomposes into the part parallel to w (i.e., p) and the part orthogonal to w.
The orthogonal part e can be seen as the amount v "erred" in modeling w. Important: Notice that e is the shortest when it makes a normal angle with w by simple geometry; this fact lies at the heart of our optimization method. The parallel part p is some multiple of w, so p = aw for some scalar a. OK, so far so good, but what a is supposed to be? Third Leap: Use the following lemma.

Lemma: two vectors v and w are orthogonal if their dot product is zero.
Proof: by geometry; only the element-wise product of v and w remains as 0 after the dust settles.

In other words, finding a such that e = w - p = b - aw and w are orthogonal means finding a such that: 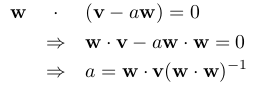. What a nice closed form! The situation is exactly the same when we project onto a subspace A instead of w; the multiple will be a vector x instead of a scalar a, and the solution is (the "dot product" of two matrices is simply the product with the left one transposed--I'll use A' to express A transposed).

Coming back to our original task, we wish to find a 2x1 vector 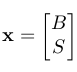such that the error e = b - Ax is minimized. In light of the above exploration, we project b onto A because the "shadow" will give us the projection Ax that is "closest" to b (keep in mind that b is an n-dimensional vector, so it's hard to visualize). The important picture below is given by Strang, and it's well worth studying carefully.

It's a simplified version, but make sure you understand every part of this picture. The "target" b is outside the column space of A, so there is no x in the row space of A that will directly yield Ax = b. Instead, we decompose b into p and e by finding the projection p. (Aside: The error vector e has to be in the left null space by the Fundamental Theorem because it is the orthogonal complement of the column space. The null space is {0} on the assumption that the two columns of A are independent.) This p is in the column space, so we will find an approximate x in the row space that will yield Ax = p.

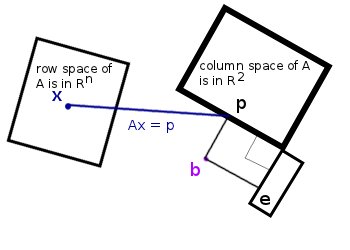
The Solution

We can't solve Ax = b exactly. But we know the vector Ax closest to b comes from the x that yields the error vector b - Ax orthogonal to A, implying A'(b - Ax) = 0. This gives A'Ax = A'b, and thus x = (AA')^{-1}A'b is the bias and slope we want for the function f. The only condition for AA' to be invertible is that the two columns are independent, so we're safe. When we expand A'A and A'b in A'Ax = A'b, we come to the conclusion that the line defined by x = (B,S) minimizes the error when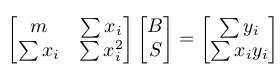
.

Final Jump: Now now now... Where does the "least squares" come in? This choice of x minimizes the squared length of Ax - b (how much we screw up) because this vector is the hypothenuse of the right triangle formed by Ax - p and e; Ax - p, being in the column space, has to be orthogonal to e, which is in the left null space. This gives us , where we note that the length of Ax - p can only be positive and therefore Ax - b is minimized by choosing Ax = p.

Calculus approves! Minimizing the squared length by differentiating with respect to B and S results in the system of equations

,
exactly the same as the result we arrived by projecting b onto A.

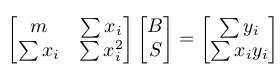Demonstration

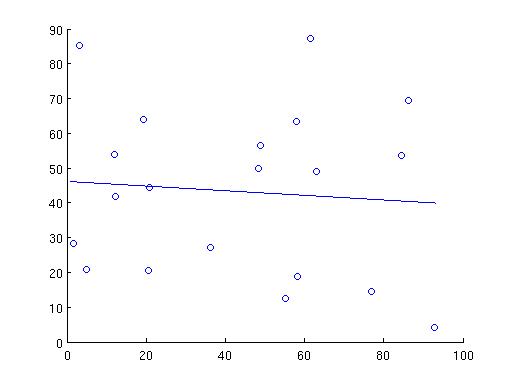
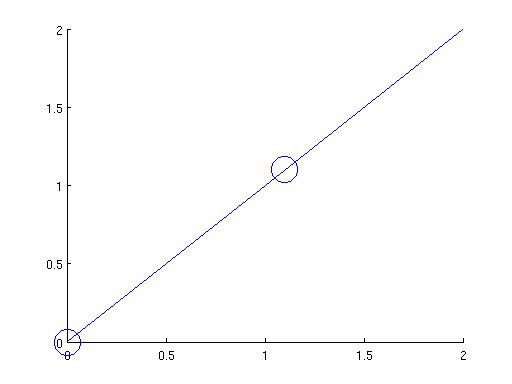
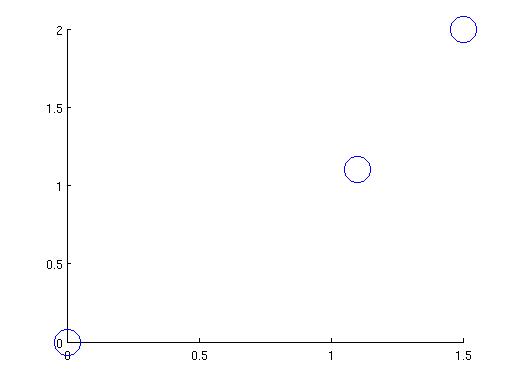
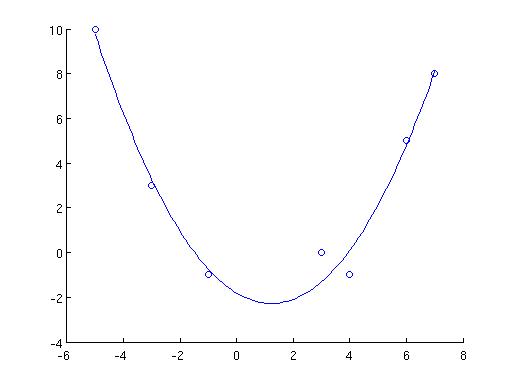
Does it work? Well, for the example in the beginning, we couldn't fit the three points (0,0), (1.1,1.1), and (1.5,2) with a straight line. This one-liner in matlab,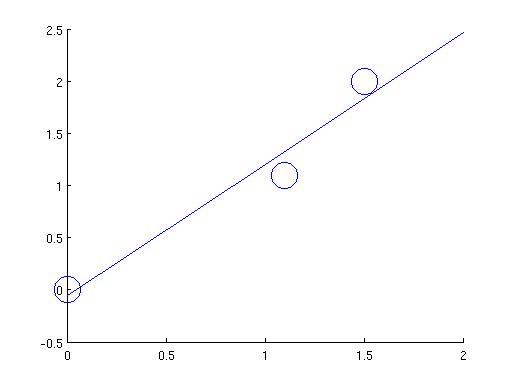
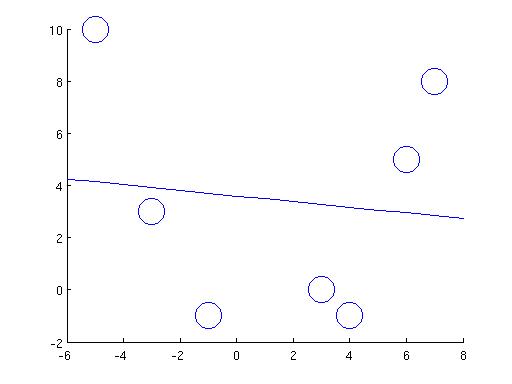
x = (A'*A) \ (A' * b),
basically solves it for us, giving the bias B = -0.0608 and the slope S = 1.2624 for x = (B,S). Here is the picture:
Notice that this is the picture where you have minimum "overall" vertical distance from the points and the line. We can fit many more. With seven points (-5,10), (-3,3), (-1,-1), (3,0), (4,-1), (6,5), and (7,8), x = (3.5973,-0.1074):
Hmm... This is still the "best" straight line, but for this system a non-linear function h(x)=B + S1 * x + S2 * x^2 might do much better in fitting these scattered points. Behold the power of linear algebra: since h is still a linear combination of the unknowns B, S(1), and S(2), we can still do it exactly the same way!

1. We want to find B, S(1), and S(2) such that the following is satisfied:

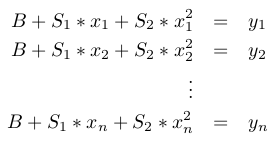
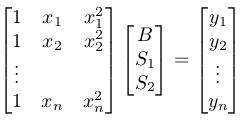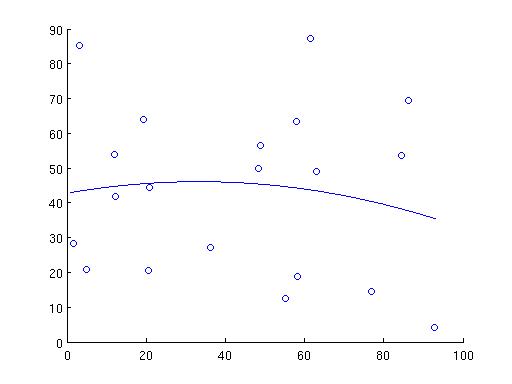
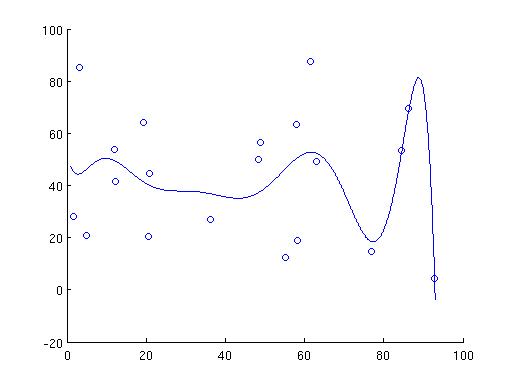
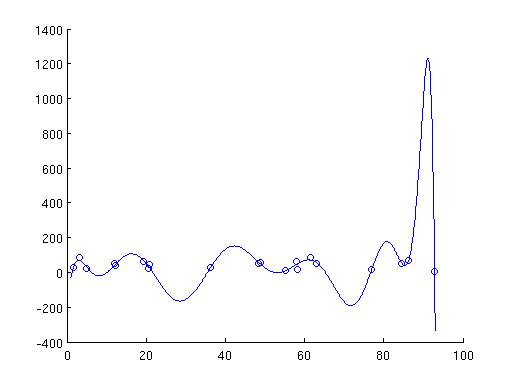
2. Realize that this system can be written in matrix multiplication
.
Then the exact same single-liner x = (A'*A) \ (A' * b) produces x = (-1.8121, -0.7624, 0.3108) with this new definition. It is clear from the picture that the function is doing a superior job of minimizing the vertical error distances:

In fact, while at it, let's make it fully general. We fit a polynomial of power m-1 to the points. When m=2, it is a straight line. When m=3, it is a parabola. The new definition of nxm A and mx1 x is driven by the following goal:

1. We want to find B, S(1), ..., S(m-1) such that the following is satisfied:

.
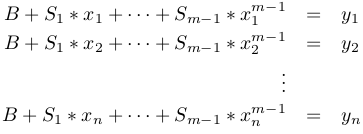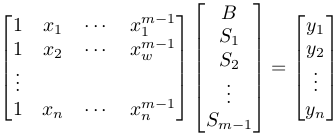2. Realize that this system can be written in matrix multiplication
.
Again, the one-liner x = (A'*A) \ (A' * b) does all the job! Let's try to fit a polynomial to a 20 randomly generated points in [100,100], for powers 1, 2, 10, and 20.
Notice that as the power goes up, the curve fits all the points more accurately. This doesn't mean it represents the actual behavior of the data -- only the observed behavior (overfitting). The computation of the bias and slopes is an elegant instance of parameter estimation; it does it in one conceptual step.

Conclusion

There are more even more amazing closed form solutions for A when it has orthogonal columns (this can be achieved by the Gram-Schmidt process, which is a canonical example of iteratively finding the pieces of "dimensional skeleton" one by one, securing orthogonality). Perhaps there will be further tutorials on the stupendous magic of linear algebra and its power to visualize and exploit the geometry of vectors, but for now, LSA was a cute enough instance of the magic.