| |
 Motivation: Traditional approaches to secure computation begin by representing
the function f being computed as a circuit. For any
function f that depends on each of its inputs, this implies a protocol with complexity at
least linear in the input size. In fact, linear running time is
inherent for secure computation of non-trivial functions,
since each party must ``touch'' every bit of their input lest
information about other party's input be leaked. This seems to rule
out many interesting applications of secure computation in scenarios
where at least one of the inputs is huge and sublinear-time
algorithms can be utilized in the insecure setting;
private database search is a prime example. In this work
we ask the question whether this gap between the efficiency of insecure and secure algorithms for the same task can be bridged, i.e. whether we can have a protocol with sublinear computation complexity in the size of its inputs.
Motivation: Traditional approaches to secure computation begin by representing
the function f being computed as a circuit. For any
function f that depends on each of its inputs, this implies a protocol with complexity at
least linear in the input size. In fact, linear running time is
inherent for secure computation of non-trivial functions,
since each party must ``touch'' every bit of their input lest
information about other party's input be leaked. This seems to rule
out many interesting applications of secure computation in scenarios
where at least one of the inputs is huge and sublinear-time
algorithms can be utilized in the insecure setting;
private database search is a prime example. In this work
we ask the question whether this gap between the efficiency of insecure and secure algorithms for the same task can be bridged, i.e. whether we can have a protocol with sublinear computation complexity in the size of its inputs.
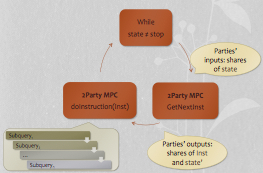
Results: We develop an approach to secure two-party computation that
yields sublinear-time protocols, in an amortized sense, for
functions that can be computed in sublinear time on a random access machine (RAM).
Furthermore, a party whose input is ``small'' is required to maintain
only small state.
We provide a generic protocol that achieves the claimed
complexity, based on any oblivious RAM and any protocol for
secure two-party computation.
We then present an optimized version of this protocol, where generic secure two-party computation is
used only for evaluating a small number of simple operations. For our optimized construction we use the ORAM protocol introduced by Ostrovsky et al. [GO'96] and Yao two party computation. For the purposes of our protocols we also introduce the notion of
shared oblivious PRF (soPRF) where the input message, the key and the output
PRF value are shared between two parties, and give a construction based on
the oblivious PRF of [FIPR'05].
|
