The Theory

The first part of this task is understanding how different face probabilities translate to different outcome possibilities. If a die has F faces, then there are 2^F possible combinations of faces that can be used to specify an outcome. (For irregular dice, we'll adopt the convention that the downward face, i.e., the one touching the rolling surface, is the outcome.) We will define the discrepancy of a particular set of probabilities as follows:

• Arrange the total probabilities in increasing order $p_1,\ldots,p_{2^F}$. Note that p₁=0 (no faces included) and p_2^F=1 (all faces included).
• Calculate the discrepancy $D = \max\limits_{i}~(p_{i+1}-p_i)/2$

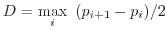
For example, Suppose we had a four-sided die with face probabilities 0.05, 0.1, 0.3, 0.55. The sixteen possible sums are, in order 0, 0.05, 0.1, 0.15, 0.3, 0.35, 0.4, 0.45, 0.55, 0.6, 0.65, 0.7, 0.85, 0.9, 0.95, 1. The maximum difference of the probabilities is 0.15, so the discrepancy is 0.075 or 7.5%. (Can you think of a way to improve the discrepancy by adjusting the probabilities?) Note that this is better than the 8.3% discrepancy of a regular 6-sided die. The discrepancy represents the worst-case difference between a target probability and a probability achievable with a single roll of the die.

Warm-up exercise: Show that no 5-sided die can achieve a discrepancy 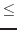$\leq$ 1%.