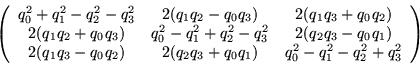3D Motion Model - Rotation

The 3-D rotation is defined as the relative rotation between the object reference frame and the current camera reference frame. This is represented using a unit quaternion, from which the rotation matrix (R) can be generated:

$$\left(\begin{array}{ccc} \footnotesize q_0^2 + q_1^2 - q_2^2... ...\footnotesize q_0^2 - q_1^2 - q_2^2 + q_3^2 \end{array}\right)$$ (16)

The four elements of the unit quaternion only have three degrees of freedom due to the normality constraint. Thus, all four cannot be estimated independently; only a nonlinear constrained minimization will work to recover the quaternion directly. Since the EKF utilizes a linearization at each step, the nonlinear normality constraint cannot be rigidly enforced within the EKF computational structure.

However, a 3-parameter incremental rotation representation, similar to that used in [11], can be used in the EKF to estimate interframe rotation at each frame. Incremental Euler angles centered about zero (or discrete-time ``rotational velocity'') do not overparameterize rotation and are approximately independent and therefore can be used reliably in a system linearization.

The incremental rotation quaternion is a function of these three parameters:

$${\bf\delta q} = \left(\sqrt{1-\epsilon},\omega_X/2,\omega_Y/2,\omega_Z/2\right)$$ (17)

$$\epsilon = (\omega_X^2 + \omega_Y^2 + \omega_Z^2) / 4$$ (18)

This incremental rotation can be computed at each frame and then composed with an external rotation quaternion to maintain an estimate of global rotation. The global quaternion is then used in the linearization process at the next frame.

Thus, we have,

$$(\mbox{\rm interframe rotation}) = \left(\omega_X,\omega_Y,\omega_Z\right)$$

$$(\mbox{\rm global rotation}) = \left(q_0,q_1,q_2,q_3\right)$$

where interframe rotation is part of the EKF state vector and global rotation is maintained and used in the linearization at each step.