Homework 4: Genetic Programming

Project: Othello

Othello is a kind of computer board game. You play on a square 8x8 gridded board, with one player white, the other is black. The key rule of this game is to surround your opponent's pieces, and then all of his pieces that are between two of yours become yours, and the one who has more pieces in the end of the game wins the game.

The goal of the project

  • Compare, contrast and discover methods to approach Othello with Genetic Programming(GP) method.
  • Investigate methods to evaluate the resulting Othello players.

    • In other words, by applying Genetic Programming method, we will train the players(actually they are computer programs) to play Othello. Some variations are made both on the hypothesis and learning method, add new terminals for GP trees, and make some experiments with varying some parameters, namely, the population size, the number of generations and the proportion of crossover. In the end, we also try to evaluate the resulting function trees(the Othello players) by playing against random player.

    Genetic programming(GP) is a variant of genetic algorithms that evolves computer programs represented as tree structures. It is a kind of evolutionary computation in which the individuals in the evolving population are computer programs. The fitness of a given individual is evaluated by executing the program on the training data. In this Othello project, genetic programs are basically formulas that use statistics of the game board, such as the number of white pieces, the number of black pieces, etc., to calculate the next board position which calculates to the best score.

    The variations on the hypothesis

    The original hypothesis
    The original hypothesis includes the following functions and terminals:

    The Modified hypothesis
    Some positions on the board are special, for example, the position that one piece away from the corners, we can simply call it white_second_corners and black_second_near_corners, I have incorporated these positions as new terminals in this modified hypothesis. Thus the modified hypothesis includes the following functions and terminals:


    In order to implement this new hypothesis, GPOthello.java, OthelloBoard.java, OthelloGPPlayer.java, OthelloPlayer.java are modified. Compare the new hypothesis with the original hypothesis
    Training configuration is as below, and it is training against random players.

    The best Trained Player based on this new hypothesis is:
    Figure 1:



    The best Trained Player based on the original hypothesis is:
    Figure 2:



    When the above two players play against each other, the player trained based on new hypothesis wins the game.
    When played against random players, the above best player trained based on new hypothesis wins 36 games out of 50 games.
    however, the best player trained against random player based on the original hypothesis only wins 23 times out of 50 games.
    ----------------------------------------------------------------

    Vary the population size, the number of generations and the proportion of crossover

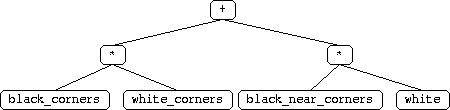
    The best Trained player based on the above new hypothesis and the training configuration below is shown in figure 3.
    PopulationSize = 50
    NumberOfGenerations = 11
    CrossoverProbability = 90
    TerminationFitness = 50
    GoodRuns = 5

    Figure 3:


    this player wins 26 games out of 50 games when it played against random player.

    The best Trained Player based on new hypothesis and the training configuration below is shown in figure 4.
    PopulationSize = 20
    NumberOfGenerations = 7
    CrossoverProbability = 90
    TerminationFitness = 50
    GoodRuns = 5

    Figure 4:

    this player wins 25 games out of 50 games when it played against random player.

    I made more experiments which training the players with different population size, different number of generations, and different crossover probabilities. The result is shown below as a table. The last item, Wins(/random), means the number of games wined by the best trained player when it played against random player.

    PopulationSize NumberOfGenerations CrossoverProbabilityWins(/random)
    207 9025
    50 7 90 26
    100 7 90 27
    150 7 90 28
    200 7 90 28
    200 31 90 31
    200 51 90 36
    200 71 90 38
    200 51 80 34
    200 51 70 28
    200 51 60 24

    Conclusion

    In this project, the evolving method is based on evaluating each genetic program, assigning each individual a fitness score after 5 games played against randem players.
    When the number of generations and crossover probability are given, then the best trained player trained based on larger population size has better performance.
    Given a fixed population size and crossover probability, then the best trained player which is trained based on larger number of generations performs better.
    Given a fixed population size and fixed number of generations, the best player which is trained based on larger probability of crossover, performs better.