To learn about Genetic Programming we used a package assembled by Eleazar
Eskin called GPOthello (Genetic Programming Othello). The package used an
Othello interface written by Astro Teller and a GP package out of Stanford.
The goal of the project was first to learn about GP and secondly to create
cool "genetically grown" Othello players that would rock Edgar's world. (Edgar
is explained below)
Machine Learning algorithms typically search the possible hypothesis space of solutions for a given problem to find a suitable hypothesis that both generalizes over unseen examples and fits the training examples well. The genetic algorithm approach is no different. It can be visualized as a heuristic search algorithm that uses as a heuristic the previous good solutions slightly modified.
Simply the process starts with a randomly generated population (set of programs) or
rules. These rules are constructed out of all the possible letters/operations specified by the
experimenter. This is one inherent disadvantage of GP's in so far that they do not
evolve their own letters or operations. There is some lee-way in that almost all Machine Learning
methods utilize a limited feature set from which they compute rules or models.
One such possible exception are Neural Networks which utilize direct sensory input
(but can also use feature vectors). Examples of letters and operators are shown below.
| + | addition operator |
| * | multiplication operator |
| 10 | constant 10 |
| larry | variable larry |
| moe | variable moe |
The letters and operators were assembled into LISP-esque structures like ( + larry moe ) in prefix notation. The sentence ( + larry moe ) would represent the target function of T = larry + moe. The set of all possible rules is infinite, but using the heuristic or bias of only choosing the best out of a given population and applying transformation rules to them tends to lead to populations that progressively get better and better at a given task such as playing Othello.
The transformation rules when applied are often referred to as cross-over between populations.
Cross over between populations is achieved by selecting two potential parents and swapping
subtrees (I do not know why two is the magical number.) It may help to visualize two rules as
trees. I give the example of ( + larry moe ), and
( * ( - larry moe) ( + 10 10 ) ).
+
/ \
/ \
larry moe
|
*
/ \
/ \
/ \
- +
/ \ | \
larry moe 10 10
|
| ( + larry moe ) | ( * ( - larry moe) ( + 10 10 ) ). |
First a subtree from each tree is chosen to be swapped. For this example I have chosen to
nominate moe and ( + 10 10 ) to swap. There are many methods to determine which subtrees
to switch, but currently random subtrees are chosen in this example. The resulting trees and
functions are illustrated below.
+
/ \
/ \
larry +
| \
10 10
|
*
/ \
/ \
/ \
- moe
/ \
larry moe
|
| ( + larry (+ 10 10) ) | ( * ( - larry moe) moe ) . |
The two parents are chosen by a fitness measure. The fitness measure is a way of choosing
the best parents out of population. Essentially a survival of the fittest technique. If
a function does a good job comparatively amongst its generation then there is a good chance
it will be chosen to reproduce. Conversely if a rule performs poorly then there is a low chance
that it will be chosen to directly affect the next generation. There have been many modifications
on this algorithm. For example the best set in a population may continue on to the next
generation without being modified, or only the best performing (1-2 rules) may be chosen to
do all the reproducing. All of these modifications affect the overall performance of the system.
For the Othello problem the default set of letters and operators is defined to be.
| + | addition operator |
| - | subraction operator |
| * | multiplication operator |
| % | modulo operator |
| white | # of white pieces |
| black | # of black pieces |
| white_edges | # of white edge pieces |
| black_edges | # of black edge pieces |
| white_corners | # of white corners pieces |
| black_corners | # of black corners pieces |
| white_near_corners | # of white near-corner pieces |
| black_near_corners | # of black near-corner pieces |
| 10 | constant 10 |
The initial defaults for the population were size of 200, growth to 31 generations with a cut-off of 50 (A goal fitness for the population. To stop growth quicker). The first run was a little confusing until I learned about the cut-off because the program would halt after 1-2 generations instead of after 31 as was specified in the file.
The best evolved player from the initial setup was
( + black_edges white ).
The first thing I did to get an understanding of GP was to vary the population sizes and number of generations. Since I was more interested in the effect of evolving a population over time I decided to go with smaller populations over more generations. I figured that having a large population (>200) would have runtimes that were far to long to test within the given time. In practice though, even the small populations did not converge very well.
The first change was to make population size 20 and set the generation limit at 200. Oddly
the first generation of this program had a higher average fitness than the last generation
(173) did.
| Generation 0 | Generation 173 |
160.00 229.00 295.00 |
110.00 407.00 250.00 |
best average worst |
best average worst |
My explanation for this is that when cross-over occurs some horrible combinations are formed. These combinations may wind up something like ( - ( + black 10 ) (+ black 10 )) which is just 0 (not a good heuristic). That would significantly affect the average. This would also account for the variability in the best player's fitness (it did not strictly get "better") .
The best player evolved from the small population/large number of generations tests was
( / ( - white_near_corners white ) ( * white black_edges )).
My next modification to the project was to vary the fitness measure, or more accurately who the tester was. In the default setup the fitness measure is a random player. The random player is not a bad fitness measure because it did wind up creating an evolved player who beats Edgar (above). I decided to play around with some variations on this, namely one mentioned in the handout evolving against Edgar, and the other being a random combination of a random player and Edgar.
Evolving players only against Edgar has an advantage in that the most difficult player
is the benchmark against which all good players are measured :). The disadvantage is that
they might only become tuned to play against Edgar and his weaknesses. One thing to
keep in mind is that Edgar is deterministic and this is a significant disadvantage. The best
rule evolved from playing against Edgar follows.
( / ( - ( * ( / ( / ( + ( - 10 white_edges ) ( + black_near_corners white_near_corners )) ( - ( + black_corners black_corners ) ( + 10 black_edges ))) ( + 10 white_edges )) ( - ( - white_edges black_near_corners ) ( - black 10 ))) ( / ( / ( * black_corners black ) ( / black_edges 10 )) ( * black black_edges ))) ( / ( + ( / black_edges 10 ) ( / ( - white_near_corners white_edges ) ( * white_corners white_near_corners ))) ( / ( / ( * white_edges black_edges ) ( * black black_edges )) ( + black_near_corners white_near_corners ))))
The second ploy was to vary the fitness measure during so that each player in a given population would play five games versus either Edgar or a random player. Which one a given player would play was based on a random integer modulo two. Because random players can play horribly (lose 64-0) and the random player is typically easier than Edgar, players who were tested against random players would have their scores adjusted by 50 points. The best player from this run was ( + black_edges white )
My final modification involved the concept of learning from losers. Basically I would
first evolve horrible players that would lose to Edgar or a random player 64-0 or something
close. This took significantly less time than it took to evolve a good player. When testing
against Edgar it only took one generation to evolve a player who lost completely to Edgar
versus 74 generations. The loser was represented as
( / ( + ( + ( * ( / white_near_corners white_corners ) ( / black_corners black_near_corners )) ( / ( + white_edges white_near_corners ) ( * black_edges black ))) ( * ( + ( / black_edges black ) ( * white white )) ( * ( * black_corners black_near_corners ) ( / white_corners black_corners )))) ( + ( * ( / ( + black white_near_corners ) ( + black_near_corners black_corners )) ( / ( * white_corners white_near_corners ) ( * black_edges black ))) ( - ( / ( + white black_near_corners ) ( - black_corners black_near_corners )) ( + ( * black white ) ( * black_near_corners white_edges )))))
I also created a losing rule from playing against random players. It was represented as
( * ( - ( - ( + ( * black white_corners ) ( + black_corners white_edges )) ( / ( * black_near_corners black_corners ) ( * black_edges 10 ))) ( * ( - ( / black_near_corners white_near_corners ) ( + black_near_corners black_edges )) ( * ( / black_near_corners black_near_corners ) ( / black_corners white_corners )))) ( / ( + ( - ( + black_near_corners black_edges ) ( + black white_corners )) ( * ( * white white_edges ) ( - white white ))) ( + ( / ( * white_near_corners white ) ( - 10 10 )) ( - ( + white_near_corners black_corners ) ( / white_near_corners white )))))
Both of these poor Othello players lost completely (i.e. 64-0). They are difficult to visualize because of their length. There is a part of the package that draws a function tree from a rule set but I have been unable to get it to work without freezing. In any case these rules were then incorporated into GPOthello and used as a fitness measure. The end result being that players were grown to destroy these losers and then tested against random players and Edgar to see if learning from losers could take place.
The best evolved player from the initial setup didn't play too badly. It lost pretty badly to Edgar (56-8), but beat the random player with a score of (53-11). If this player would have won versus Edgar it would have been more luck than anything. Luck is a possible factor in these tests because of the randomness of the initial population. It is possible that the entire first generation was composed of Edgar-beaters it would stand a good chance that an Edgar-beater would have evolved. But it appears that luck was not on the side of this evolved player.
The best player evolved from the small population/large number of generations tests was an exceptional player. It beat the random player 43-21 and also easily won against Edgar 51-13. Again this player never even saw Edgar at any point in its development. It is more a matter of luck that it was able to beat Edgar. An important detail to notice is that it beat the random player by a small margin than the player above did (43-21 versus 53-11), but was able to generalize Othello enough to play against Edgar and win. It would be good to think of the random player as the training examples and Edgar as the testing or verification example set. This rule set was able to generalize better over unseen examples than the initial setup.
After evolving from just playing Edgar it is shown that it is possible to evolve an Edgar-beater by just knowing and playing against Edgar. The function described in a section above was able to beat Edgar 53-11 but lost to the random player 25-39. Again it would appear that this rule set did not generalize well over unseen players since it lost to the random player which it did not see during its training.
The random fitness measure lead to a player who beat a random player 64-0 and lost 8-56 versus Edgar. This may have been a result of a good evolved player scoring a 50 (i.e. beating a random player 64-0) but then being eliminated by Edgar in the next generation. That might be possible because the best from one generation was automatically placed in the next generation without any modification. It is also possible, but unlikely, that the final evolved player (and its ancestors) only saw random players throughout the evolution and never played against Edgar. This is a possibility but more than likely the life span of a GP player was only one or two generations.
Training with a fitness measure consisting of a GP player who lost badly to random players resulted in a player who was still unable to beat Edgar but did so without getting shut out (6-57). The interesting development though was that the evolved player was able to beat a random player (41-23). Another interesting point of this is that it matured (i.e. stopped getting better) after 12 generations. So total runs to develop a random player-beater from a loser was 13 generations versus 3 with a fitness measure consisting of random players.
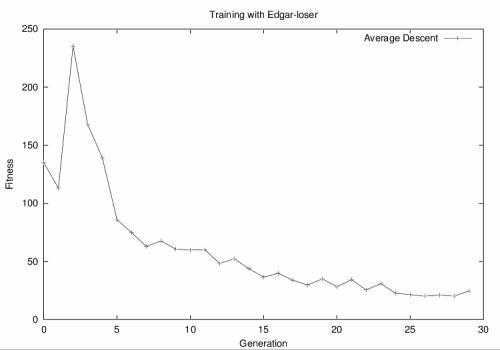
Training against an Edgar-loser lead to an evolved player who was able to beat random
players 52-12, but lost to Edgar 17-47. An example of the descent of the evolved population's
average fitness is shown below.

It is rather interesting that you can shape/train a population by only giving it a loser. What is cooler still is that you can shape/train that population pretty well (i.e. there is some usefulness to it.) In this instance its usefulness was the ability to train a moderately good player that could beat up a random player. It is more inefficient than the standard fitness measure by taking 13 runs to create a moderate player versus 3 runs with a fitness measure consisting of a random player.
After toying around with some of the simple parameters of the Othello Project I find that I am interested in the diversity of the population of players. For instance if I gave a fitness measure that did not allow a converging population (e.g. randomly assigned fitness) how much diversity could be brought into the group? Perhaps it's easier to visualize like this. Imagine that my goal is to create a population of 200 very distinct individuals. I want to make sure that each program is completely distinct from any other.
This may not make sense within the Othello framework, but envision it within an A-Life setting. Each 2D grid has different floaters,... and at no point in time will any two boards look alike. This way I could assign a name to each board, write down its rule set and come back in a while and still be able to identify each board correctly. It would be an interesting machine learning problem from both aspects. First creating a diverse enough population, and secondly finding a learner that will find each individual's unique rule set, and later identify it properly. --------------3171C86B5C766DB55961F874