ABSTRACT

In this paper, we employ genetic programming to evolve Connect-4 players.  A players skill level (fitness) is  based on how the player
performs when placed in competition with other randomly chosen  members of the population.  Different emerging game strategies are
observed as the players evolve and their skill improves.

1.  Introduction
 
Connect-4 is a popular board game that many played as children.  The game is played on an eight  by eight   board.  A legal move is placing
a piece in an empty square so that the piece is either at the bottom row of the playing board, or directly on top of the highest piece in any
column.  The first player capable of placing four their pieces adjacent to one another either vertically, horizontally or diagonally wins the game.
 A game may be composed of many moves.  Because of the difficulty of attributing the effect of a single move on the final result of the game,
fitness evaluation is based on the final result of a game.   This indicates that the evolved player has to find some general concept behind playing
Connect-4 in order to play competitively.

Since we do not have an optimal solutions to the Connect-4 board game there is no absolute measure that the evolved players can be measured
against.    In order to determine the quality of the evolved genetic programs, they are tested against each other, random players, and human players.
 General trends in good players are observed and are used to speculate to how an optimal player would behave.  We feel that the purpose of genetic
programming should be to discover these “optimal” solutions or patterns.

This paper is divided into four other sections.  An brief description of genetic programming is first given in section 2.  A description of how genetic
programming was utilized to evolve the connect-4 programs is explained in section 3.  An analysis of the experiments and the results is described
in section 4.  A final conclusion consolidates the experiments the results and possible ways have improved the process.
 
 

2.  Genetic Programming

Genetic programming is a machine learning method that was motivated by an analogy to biological evolution.  The underlying principal is similar
to that of the Darwinian theory of evolution.  The goal of genetic programming is to evolve amongst a population of hypothesis (or programs)
the most fit.  The process of evolution occurs though a sequence of generations in which the fittest survive and the weak die out.  The initial
population is typically chosen at random and certain rules are employed in order to ensure that the members are correctly behaved within the
domain of the problem.  Each member of the population is then evaluated for their fitness based on some evaluation criteria.  Members of the
population are then chosen at random  based on their fitness, and are moved to the next generation.    New members are also formed by mutation
of select members or by crossover between two existing members.  Other operations may also be employed.  As generations die out, new
generations will emerge inheriting the good attributes of their predecessors.  Members with good genetic structure will tend to be selected and
their genetic material passed on.    A typical member of a genetic program will have several input points known as terminals and several evaluation
functions known as nodes see Koza [1].  A program will be composed of some combination of select nodes and functions.  Some of the challenges
in formulating a genetic programming  models is defining these nodes and terminal to fit the given  problem.

There has been extensive research done in the area of genetic programming.  This paper utilizes ideas used in some of these research experiments.
 Craig W. Reynolds [2] performed a study on the pursuit and evasion game of Tag.  In the study competitive fitness was used to evaluate fitness
of members of the population.  Players fitness was rated on how well they performed when placed in competition with six other random members
of the population.  The purser would chase the evader and if caught role reversal would take place; the evader now becomes the pursuer and the
purser becomes the evader.  A game was composed of twenty five moves where each move the purser attempts to make a capture and the evader
attempts to escape.  The winner is calculated based on the player who was the evader for a greater number of moves.   The idea of competitive fitness
was used by in the research paper to develop an optimal connect-4 player.

Another research example was the study done by Gabriel J Ferrer and W. N. Martin [3].  The study analyzed the genetic programming paradigm in the
context of Senet, a strategy game popular in ancient Egypt.  The hypothesis representation used by the genetic programs in the population used conditional
 and logical operators.  In particular the “if” function and the logical operators and, or and, not were used.  The simple arithmetic operators +, -, and
* were also utilized.  The fitness of an individual in the population was determined by pairing two members and having them compete in three games.
 Individuals who won two games were declared winners and moved on to the next round of the tournament.  All individuals who lost at the same round
were given the same fitness.  The reason three games were chosen as opposed to a single game of competition was the  non-deterministic nature of Senet.
 The next plausible move  is determined based on a combination of a  probabilistic drawing factor in conjunction with the genetic programs selection of
the next best move.  The research was able to produce effective players at the game of Senet.

3.  Genetic Programming implementation

A pre-built Java based genetic programming package GPJPP written by Adam Fraser and Thomas Weinbrenner was used to implement the Connect-4
problem.  The package is flexible enough to allow the user to define the problem and the primitives to use for the genetic program representation.
 The following terminals and nodes were used in the formulation of the problem domain.

Function Nodes
 
 
 

Node	Number of Input Terminals	Description
+	2	Addition Operator
-	2	Subtracion Operator
*	2	Multiplication Operator
%	2	Safe Division Operator

Terminals
 

Terminal Value	Description
w	number of white pieces currently on the board
b	number of black pieces currently on the board
W	number of white pieces on the edges (row 1 or row 8 or column 1 or column 8)
B	number of black pieces on the edges (row 1 or row 8 or column 1 or column 8)
c	number of white pieces on the corners (there are four corners on the board)
C	number of black pieces on the corners (there are four corners on the board)
n	number of white pieces near the corner (the three squares around the corner)
N	number of black pieces near the corner (the three squares around the corner)
e	number of white pieces near the edges
E	number of black pieces near the edges
j	number of adjacent white pieces (total number of pieces that are directly adjacent)
J	number of adjacent black pieces (total number of pieces that are directly adjacent)
10	A constant used to adjust weights

 

The re is a total of thirteen terminals.  The more terminals that a problem is given the more time and generation which are required to evolve a player
with the required fitness measure.  Many of the primitives used here were also used in a previous research effort for the Othello board game (see http://www.cs.columbia.edu/~eeskin/othello/).  An additional terminal was added “j” and “J” to allow for an understanding of pieces being adjacent
to one another.  Notice that the selection of these nodes is very critical to the resulting player.  If the selected nodes/terminals do not conform to the
problem at hand, genetic programming will only be able to discover mediocre players.

After each move statistics on the board are collected to determine the new value of the terminals.  The evolved player is presented with the value of these
terminals and all the currently possible legal moves.  Based on the players evolved program a decision is made as to what the next move is.  An example
of an evaluation function is  “(+ 10 E).” Which adds 10 to the number of black pieces near the edges to select the next move.

One of the limitations that the genetic package introduced was a natural way to allow competitive coevolution of the players with other players in the population.
 The package evaluates the fitness of a player as soon as it is created without consideration that other members of the  population have not been created.
 To overcome this problem we used a previous generation to evaluate the fitness of the current generation.  The very first generation has its fitness measured
against random players.  The fitness of  players is evaluated by competition against six other players.  Based on the number of games that the player wins
and the duration of each game, the player is assigned a fitness measure.  Shorter games are assigned higher fitness (an assumption is made that better
players will tend to win the game faster).

The learning cycle ends either when a fixed number of players with fitness measure higher than a pre-specified value are evolved or when the maximum number
of generations is reached.
 

4.  Results

Several evolution runs were conducted using the design above with minor variations between the runs.  The population size and the number of generations
were fixed through out the runs.  Three runs will be discussed here and the different learned concepts as the player evolves will be analyzed.

4.1  Run A

In this run the genetic program was evaluated for fitness by playing against a random player.  Several interesting patterns were observed amongst the
evolved players.  Random players determine the next move by  randomly choosing a move among the set of current legal moves.  The evolved players
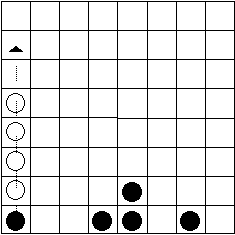
for this scenario had a tendency of lining up their pieces directly on top of each other as illustrated in the diagram below.

Genetic Program Playing White, Random Player
Competing as Black.

Most players would start at the right column and stack the pieces on top of each other.  Although this strategy is simple it was very effective when
used against the random player.  This technique resulted in the computer defeating the random player in  49 out of 50 games (or a 98 % win ratio).
  Because of this ratio the proceeding generations did not have to evolve dramatically in order to defeat the random player, as long as they used
the same basic strategy they were almost guaranteed victory.  The above strategy is so simple that when we competed directly with the evolved
player we found that defeating it next to trivial.  A sample genetic program that used this technique was a one terminal function

RPB: white_edges

Among all the evolved functions none used the terminals “white” and “black.”  The reason for that becomes obvious when the rules of Connect-4
are re-observed.  Since the players alternate moves the number of black pieces will always be equal to or one piece greater than the number of
black pieces on the board
 

4.2  Run II

In this run we employed some modification to the fitness measure.  In particular so that players compete against other members of the population.
 We felt that this way would produce better players than competition against random players.  The fitness measure depended on two factors:  The
complexity of the Genetic Program tree, and whether the game was a win, a lose or a draw.

To our surprise the resulting strategies were similar in many ways to those observed in Run I.  There were however enough relevant differences.
 The major difference was the use of white_adj_pieces as a terminal to some of the evolved players.  This produced a strategy in which the players
not only place the pieces vertically on top of one another filling one column at a time, but also attempting to maximize the number of adjacent pieces.
 When we competed against the player we found it attempting to place its pieces close to one another horizontally or diagonally portraying this
simple strategic approach.  This approach was again very effective against the random player, yet can be easily defeated when we competed
against it.

Below are samples of some of the evolved players:

RPB:  ( - black_adj_pieces  white_near_corners)
RPB:  ( - black_corners       white_near_corners)

4.3  Run III

Most of the genetic player produced by Run I and Run II were short trees.  We felt that these short trees are incapable of capturing the general
concept behind playing the Connect-4 game, and that more complex trees would have to be developed.  Since our fitness measure penalized more
complex solutions, this fitness measure was removed.  In order to reward efficient players, the number of moves required untill victory were used
for the fitness measure, longer game resulted in worst player fitness.

Below is a sample of one of the evolved players

RPB:  ( -   black_edges  ( +  ( -  ( *   white_edges   white_near_corners ) ( -   10   white_corners )) ( /  ( +   white_corners   white_near_corners )
( /  ( +  ( /  ( -  ( +   white   black_adj_pieces ) ( /  ( -   white_near_corners   white_edges ) ( /  ( -   black_adj_pieces  ( -   white_near_edges   10 ))
( /   10   white_near_edges )))) ( /   black_near_corners  ( /  ( +  ( -  ( +  ( +   white_near_corners   white_near_edges ) ( *  ( *   white_near_corners
 black_near_edges ) ( -   black_adj_pieces   white_corners ))) ( -   white_near_edges   black_near_corners )) ( *  ( +   white_corners   white_near_corners )
( -   black_adj_pieces   white_corners ))) ( /   white_near_corners   black_near_edges )))) ( /  ( *  ( *  ( /   10   black_near_edges ) ( +   white_corners
 black_corners )) ( -  ( -   white_near_corners   white_edges ) ( /   white_near_corners   black_near_edges ))) ( -   black_adj_pieces   white_corners )))
( *   white_edges   white_near_corners )))))
 

There was a tendency for all of the developed players to be as complex as the above sample player.  This player was evolved in generation 21 and was
able to survive for several more generations.  When we competed against this player we found a dramatic improvement in performance in playing tactics
over Run II and Run I players.  Although the player was much more competitive and made some surprisingly good moves, it was still at a high enough
level of competition to be able to always defeat us (although on occasion it did).  When compared to the random player, this player won all of the fifty
played games.

5.  Conclusion

Evolution of a good board game player is highly dependent on the interplay between the fitness evaluation measure, the selected terminals and nodes,
and the training partners used for training competition.  Different variations on these elements can have dramatic effects on the resulting players. In
order to produce a highly skilled player the terminals and nodes have to be general enough to allow formulation of the game concept.  However,
one must be careful not allow for too many terminals and nodes otherwise it will take longer times to evolve the players.

In this paper we were able to evolve good players that were easily able to defeat the Random player.  The player’s skill level was not enough to
be able to compete effectively against a human competitor. We feel however, that with more variations on the genetic program model a very good
player can be evolved.  This was observed as the player continuously improved over time with these variations.
 

References

[1]  Koza, J. R., 1992.  Genetic Programming:  On the Programming of Computers by Means of Natural Selection, MIT Press.

[2]  Craig W. Reynolds.   Competition, Coevolution and the Game of Tag.   Proceedings of the Fourth International Workshop on the Synthesis
and Simulation of Living Systems, pp. 59-69, MIT Press,   6-8 July 1994.

[3] Gabriel J. Ferrer and Worthy N. Martin.   Using Genetic Programming to Evolve Board Evaluation Functions for a Board Game.   1995 IEEE
Conference on Evolutionary Computation, Vol. 2, p. 747, IEEE Press, 29 November - 1 dec 1995.

[4] Frank W. Moore and Oscar N. Garcia.  A Genetic Programming Approach to Strategy Optimization in the Extended Two-Dimensional
Pursuer/Evader Problem.   Genetic Programming 1997: Proceedings of the Second Annual Conference, pp. 249-254, Morgan Kaufmann,
13-16 July 1997.