Application of Two Layer Supervised Back Propagation Neural Networks to Edge Detection in Still Images

Jack Huang
Jiawei Fang

May 13, 1999

1. Introduction

Edge detection has been a field of fundamental importance in digital imaging research. Edges can be defined as pixels located at points where abrupt changes in gray level take place. By marking the edges of individual objects, an image can be segmented; the individual segmented objects can be indexed and classified; and semantic characteristics of the image can be identified.

Neural networks often provide important insights in developing new algorithms and take on key roles in real-time expert systems, but its application to image processing in general is not very well studied, perhaps due to the lack of practical applications. In this paper, we attempt to use neural networks as a system for image processing, namely for edge detection. By applying BPNNs to a problem as well defined as edge detection, we are allowed to uncover neural networks' abilities and limitations using an existing technique as a reference. This information can provide important guidance when building adaptive image processing systems that does exploit the strengths of neural networks.

In our study, we built training and test sets by sub-dividing several images into blocks. We train the neural networks into edge detectors with target blocks produced from the convolution of Sobel's gradient operators and the input images. Several networks result from variations in block sizes and the number of hidden nodes in the networks. We then evaluate these networks by comparing their performance on the test cases with numerical results. We then use the networks to produce edge maps to understand the qualitative context of their abilities.

Section 2 details the theories involved by our approach in preparation of this study. Section 3 provides the quantitative and qualitative results of experiments comparing several neural networks; there we provide our analysis. Section 4 concludes this paper with a summary of the results.

2. Approach

2.1 Classical Edge Detection

Typical image detection techniques in classical digital image processing uses discrete matrix operators called Gradient Operators. One such set of operators is the Sobel operators, which we use in this study to produce the target images used in training and testing the neural networks. The edges are obtained by first performing separate 2-D discrete convolutions of these operators on the original image, using the center grid as the origin. This produces two orthogonal gradient vectors, one in the horizontal direction and one to the vertical direction, at each pixel. The sum of these vectors produce a gradient magnitude, which is thresholded by the unit step function to produce an edge map of pixels whose gradient magnitudes exceed the threshold.

Sobel Gradient Operators

Vertical Operator
-1	0	1
-2	0	2
-1	0	1

Horizontal Operator
-1	-2	-1
0	0	0
1	2	1

The following images are the training set, and two test sets we used. Next to the original 256x256xgrayscale images are the edge maps produced by the Sobel filter in the GNU Image Manipulation Program. Notice how rough surfaces such as hair gets classified as edges.

Training Set (lenna)

Test Set 1 (camera and Jack)

Test Set 2 (Baboon)

2.2 Block Image Processing with BPNN

Due to the speed and space requirements associated with back propagation algorithm and neural networks in general,
we cannot allow an entire image of viable size to be fed into the BPNN without exhausting available system resources. Therefore, we need a pre-processing stage where an input image is divided into reasonably sized blocks. Each block represents an occurrence in the instance space, and is fed into a network individually for training or processing. Upon processing, the network outputs are reassembled in a post processor to yield a complete image. Only by
using this divide and conquer strategy can we utilize smaller networks in achieving acceptable results while trading off
processing precision. As a result, the size of the training and test sets is multiplied. The benefit of image processing by blocks is evident in every operation that takes into account of correlation among pixels. A smaller window size allows algorithms to effectively process local information while ignoring irrelevant pixels outside the window. In addition, the simplified networks can be more easily analyzed and understood by people conducting experiments.
The diagram below illustrates one of the edge detecting networks we trained. There are 4x4=16 inputs, each connected to 4 nodes in the hidden layer through a weighted edge. The hidden units each connect to the 16 output units. During the feed forward process, a 4x4 image block is loaded into the network as input. The hidden layer nodes extract different components of edge features by integrating the inner products of the weights and the input values. The feature components are cross correlated at the output layer, resulting in certain pixels being marked as edge points.

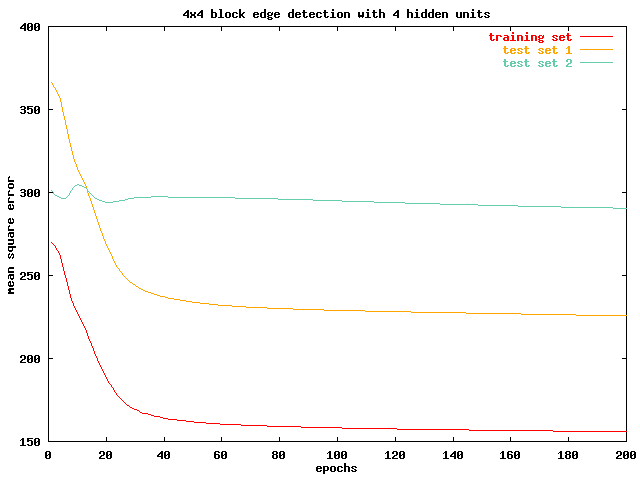
4x4 Block Edge Detection BPNN with 4 Hidden Units

Hidden Unit Weights

Output Unit Weights

3. Results

The experiment was carried out with Jeff Shufelt's neural network package, with learning rate set at 0.3 and momentum set at 0.3, using a sigmoid squashing function. We extended the package to support block operations, carry out mean square erro calculations, and load target images.

3.1 Network Performance

The following charts compare the performance of the training set and the two test sets across four different networks.
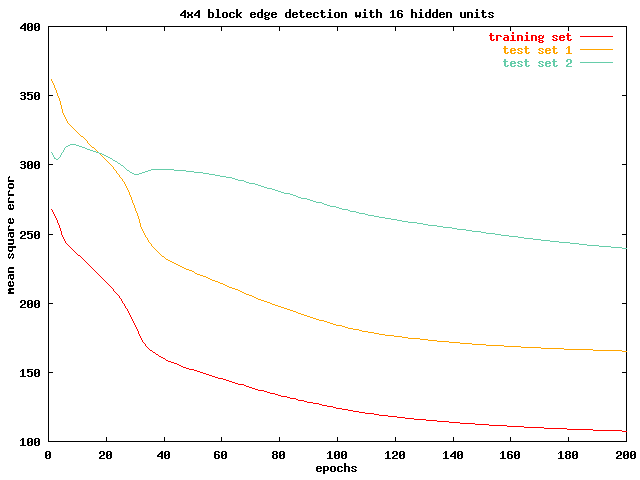
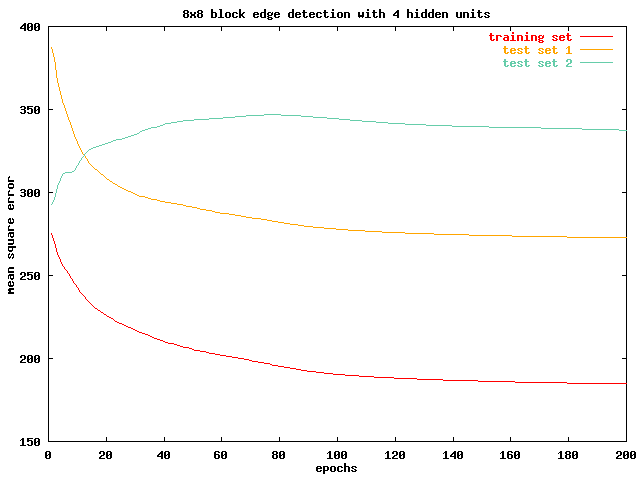
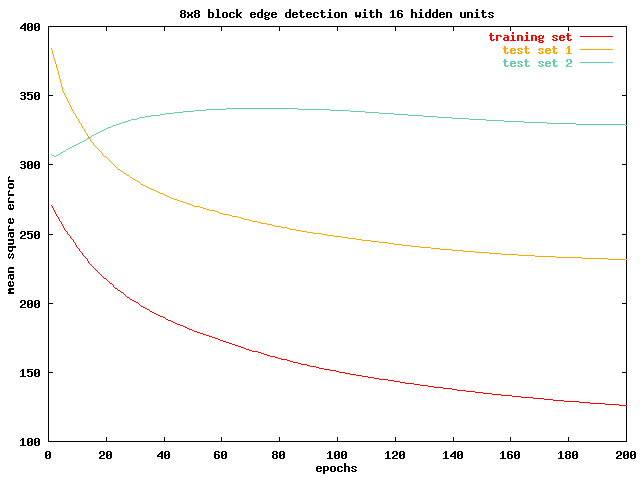
The networks vary in their input and thus output sizes, as well as the number of hidden units. In the 4x4 block network with 4 hidden units, we see virtually no gain in performance on test set 2 as the training set and test set 1 improves.
When we increase the number of hidden units to 16, at the end of 200 epochs test set 1 has outperformed itself by approximately 100, and the training set by 50, when compared to the network with only 4 hidden units. In addition, we see modest improvement on the performance of test set 2.

In the next chart, we evaluate an 8x8 block network with 4 hidden units. It is very evident that this network suffers from a learning bottle neck. All of the training set and the two test sets reaches asymptotes early on in the training process with high mean square errors. More over , the performance of test set 2 degrades steadily even as the network is being trained. The next 8x8 block network, with 16 hidden units, sees significant improvements on training set and test set 1 performance, but the pattern of performance degradation in test set 2 persists.

It appears that test set 2 contains very different features from the training set. This is evident in its poor performance in all of the four networks we investigated, and by comparing the two sets qualitatively. While lenna contains many smooth surfaces both in the foreground and background, the baboon is covered with fur. Increasing the input block size thus resulted in the network over fitting on the training set, depriving it of its ability to detect edges effectively in test set 2. Also, by comparing the result of the 8x8 block networks from the 4x4 block networks, we notice that the 8x8 block networks performs worse in both cases. As we discussed in the previous session, increasing the block size being processed will introduce extra information. We can infer from these two pieces of evidence that in edge detection, a smaller block size is always better. The extra information in the 8x8 block seems to be interfering with the edge detection process.

We also notice that increasing the hidden units in both cases introduces significant improvements in network performance. In the 4x4 block network, it evens breaks the deadlock on test set 2 performance. If hidden units are feature extractors, as we discussed in the previous session, then it makes sense that by introducing more hidden units, we create finer granularity in identifying different types of edges and increase our chance of telling edge points apart from non edge points.

3.2 Edge Maps

The following edge maps are produced by the four networks, with the map produced by the 4x4 network with 16 hidden units performing closest to Sobel. As expected, the edge map to the lower left is smothered by noise, often with entire blocks being gray. There edges are detected, but there is not enough hidden units vs block size to pin point the edge pixels. The 8x8 (16 hidden) network performs better, but in general the networks with smaller block sizes outperform the rest.

Camera edge Maps produced by, from top left, clockwise, 4x4 (4 hidden), 4x4 (16 hidden), 8x8 (16 hidden), and 8x8 (4 hidden)

The baboon is not at all recognizable in the 8x8 ( 4 hidden ) network. This is the worst performing set. The edges identified in 4x4 (16 hidden) are not as strong due to lack of coherence between the edge features of the nose and the surrounding hair.

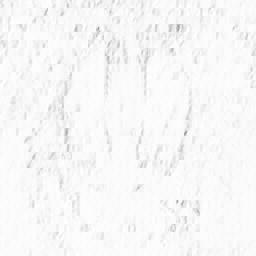
Baboon edge Maps produced by, from top left, clockwise, 4x4 (4 hidden), 4x4 (16 hidden), 8x8 (16 hidden), and 8x8 (4 hidden)

5. Conclusion

In this paper we discussed the application of BPNN in edge detection of still images, using the results produced by Sobel gradient operators as target values. We investigated the impacts of variations in network input size and the hidden layer size on the accuracy of the output edge map. We confirmed that small hidden layers and large input sizes results in general degradation of performance. In particular, large input sizes results in severe over fitting and hampers generality. We also explained that hidden units are vital to detecting the presence of edges points in an image.

It is conceivable that, with adequate training, BPNN can perform well as simulators of existing algorithms; however, the edge detectors in the networks are formed automatically without explicit knowledge of how the target algorithm works, and surprisingly, both methodologies share certain similar features. But there is a fundamental difference: while convolution with Sobel operators is used to produce edge points at each pixel, BPNN propagates pixel values and have them converge at some point to form edge points. This is added complexity in edge detection; however, it is also a key characteristic of neural network algorithms that can be exploited when information must be gathered from disconnected regions of an image. An example where is can be used is finding motion vectors in predictive compression algorithms for digital video.