Deterministic Simulation for Risk Management
Quasi-Monte Carlo beats
Monte Carlo for Value at Risk
Anargyros Papageorgiou[1] and Spassimir Paskov[2]
November 1998
Overview
Monte Carlo simulations are widely used in pricing and risk management of complex financial instruments. Recently, quasi-Monte Carlo methods, which are deterministic methods because they are based on low discrepancy sequences, have been found far superior to Monte Carlo for pricing of financial derivatives in terms of both speed and accuracy. In this paper we address the application of these deterministic methods to risk management.
Our study compares the efficacy of deterministic simulation, using low discrepancy sequences, with Monte Carlo for the computation of Value at Risk (VaR). In particular, we show how the deterministic methods can be applied to the computation of VaR and that they converge faster than Monte Carlo. We illustrate our findings with two tests. The first of our tests uses a portfolio of equity and currency european call options. The second test uses a portfolio of collateralized mortgage obligation tranches. The low discrepancy sequence chosen for our tests is the generalized Faure sequence due to Tezuka [1995].
VaR in brief
Market risk has become one of the most popular buzzwords of the financial markets. Regulators, commercial and investment banks, corporate and institutional investors are increasingly focusing on measuring more precisely the level of market risk incurred by their institutions. Market risk is the uncertainty of future returns due to fluctuations of financial asset quantities such as stock prices, interest rates, exchange rates, and commodity prices. One of the most widely accepted concepts in market risk management is Value at Risk. Risk management systems based on VaR have been designed and implemented in many financial institutions, asset management institutions, and non-financial corporations. VaR has also been officially accepted and promoted by regulators as sound risk management practice. VaR is based on a statistical approach and it quantifies the market risk in portfolios of financial instruments. It can be used as a trading and control tool. It serves a number of purposes such as information reporting, resource allocation, performance evaluation, and trading limit allocation. For a more detailed description of the reasons for the tremendous growth in market risk management, the establishment of VaR as sound risk management practice, and the various applications of VaR we refer to Jorion [1997].
VaR is defined as the maximum loss with a given confidence level over a given time horizon in a portfolio of financial instruments.
Often, the confidence level is chosen as 98% and the time horizon is assumed to be one day. Other confidence levels, such as 95%, and time horizons, such as 10 days, are also in use. Throughout this paper, VaR is assumed to be the one day maximum loss in a portfolio with 98% confidence. The 98% confidence level implies that there is only 2% probability of losing a larger amount over a period of one day. Therefore, on the average, at any day of a 100-day period we can expect to lose more than the amount of VaR in two days out of the 100.
Measuring VaR
We
now introduce the mathematical framework for VaR. Let 
be random
variables and 
be a function
that depends on them. We can think of each 
as a market risk
factor such as the percentage change of a foreign currency, the yield on a
bond, a commodity price, etc. We can think of 
as the loss
function of a portfolio that depends on the market risk factors 
. Denote by 
the cumulative
distribution function of the loss, 
, i.e., the probability of 
being less than
, for some 
.
The
problem of computing VaR can be reformulated as the problem of quantile (percentile) estimation. For a given 
(e.g. 0.98)
find 
such that 
, i.e., find 
such that the
loss 
is less than 
with
probability exactly 
(e.g. 0.98).
Then clearly VaR is given by 
. Therefore, to find VaR we need to approximate the
inverse of the cumulative distribution function at the percentile corresponding
to 
.
The approaches to VaR can be essentially divided into two groups. The first is based on local valuation of the financial instruments. The best example from this group is the variance-covariance method. This method relies on the assumption of normality of the market risk factors and delta-equivalent presentation of the portfolio. Due to these assumptions it is possible to show that there is an explicit formula for the quantile and, therefore, for VaR. From a computational point of view, this method consists of relatively simple computations that are based on matrix algebra. Without going into a full discussion of advantages and disadvantages of this method, we only mention its inadequacy for measuring the risk for derivative instruments such as options or mortgages. For example, under this method options are specified by their delta-equivalent representation, i.e., the change of the option is given by the product of delta of the option and the change of the underlying instrument. At-the-money options may exhibit high convexity that is not taken into account by the variance-covariance method.
The second group is based on the simulation approach that performs full valuation of the financial instruments. The best examples are historical simulation and Monte Carlo simulation methods. The historical simulation method is similar to the Monte Carlo method except that historical changes in prices are used rather than simulated changes based on a stochastic model. Although both methods solve the convexity problem of the variance-covariance approach mentioned earlier, the Monte Carlo method is more flexible and has certain advantages over the historical simulation method. Some of the criticism of the historical simulation method is due to: (i) the assumption that the past represents the immediate future, i.e., the distribution is assumed to be stationary, (ii) the high sensitivity of the results with respect to the length of the time horizon and, (iii) problems with collecting consistent historical data. See Jorion [1997] for a full discussion of advantages and disadvantages of these methods.
Some authors Jorion [1997] consider Monte Carlo as the most powerful and comprehensive method for measuring market risk. This method can also handle credit risk which is beyond the scope of this paper. However the most serious disadvantage of Monte Carlo is its high computational cost. This paper addresses only the computational issues of Monte Carlo. We propose that deterministic simulation using low discrepancy sequences offers a highly efficient alternative to Monte Carlo for VaR calculations in risk management.
Monte Carlo simulation
We have shown that computing VaR can be reduced to the problem of quantile (percentile) estimation. We now outline the Monte Carlo method for quantile estimation.
1. Randomly
draw 
samples from
the multivariate joint distribution of 
.
2. For
each sample evaluate the loss function 
. This results in 
simulated
values of the loss 
.
3. Construct
the empirical (sample) distribution function,
, of the loss by sorting the values
and assigning the corresponding probabilities to each
value. More precisely, 
, where 
is the number
of the 
that are less
than 
.
4. Compute
the sample quantile 
such that 
and use it as
an approximation of the actual quantile. It is possible to show that the
distribution of the sample quantile 
is normal, as 
, with mean the actual quantile 
and variance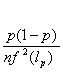 
, where 
denotes the
density function of the distribution of the loss; for the proof see Stuart and
Ord [1994].
Deterministic simulation
Can the high computational cost, which is the biggest disadvantage of Monte Carlo, be overcome using quasi-Monte Carlo methods? These methods are similar to Monte Carlo but the samples are taken at well-devised deterministic points rather than at random points. The deterministic points are uniformly spread because they belong to low discrepancy sequences; see Tezuka [1995] for the precise definitions and some efficient constructions of low discrepancy sequences.
Quasi-Monte Carlo methods can be used for the approximation of multi-dimensional integrals. Recent constructions and improvements of low discrepancy sequences have led to significant advances by reducing the high computational cost of pricing of financial derivatives, see Ninomiya and Tezuka [1996], Papageorgiou and Traub [1996], Paskov [1997], Paskov and Traub [1995]. Quasi-Monte Carlo methods achieve an equivalent performance at a fraction of the time required by Monte Carlo.
Intuitively, since VaR requires the computation of the probability of a tail event, and since the points in a low discrepancy sequence are designed in a way that reflects the volumes they occupy, it is reasonable to expect that the fraction of the low discrepancy points that belong to the tail event in question should reflect its probability fairly accurately.
We
now show how quasi-Monte Carlo methods can be used for the calculation of VaR.
Recall that 
are random variables chosen to represent the market
risk factors on which the value of a portfolio depends. The potential loss is 
and we denote
the joint multivariate distribution of 
by 
. The probability distribution function of the loss is
then given by 
, 
, where 
is the characteristic (indicator) function of the set 
.
Assume
that, by a change of variable, this integral can be transformed to one over the
-dimensional unit cube of the form 
, for a suitably chosen function 
. For instance, such a transformation is possible for
normally (or lognormally) distributed market risk factors. We can then use a
quasi-Monte Carlo method to approximate the value of this integral. The error
of this approximation is bounded by the product of the variation, 
, of the function 
and the
discrepancy of the sample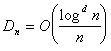 
; see Niederreiter [1992].
Given
a confidence level 
we want to
estimate the value 
such that 
. Following the outline of the quantile estimation
method presented earlier, we sample the loss function 
and we
construct the empirical distribution 
of the loss. In
particular, given any 
sample points 
, 
, the empirical distribution of the loss is given by 
. Let the 
sample points
belong to a low discrepancy sequence. Without loss of generality, assume that 
is such that 
is an integer.
We approximate 
using the value
for which 
. By the Koksma-Hlawka inequality, the bound on the
error that results from the use of the empirical distribution function is
,
where
is a constant that depends on the low discrepancy
sequence.
An estimate for 
can be derived
by analyzing 
in a
neighborhood of 
; see also the derivation of the Monte Carlo error in
Stuart and Ord [1994]. Assume, for instance, that the loss distribution is 
,
. Then applying the mean value theorem and using the
above inequality we obtain
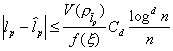, (1)
where
belongs to the
open interval generated by 
and 
.
This may be compared with the expected error of Monte Carlo which is
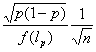. (2)
If we
compare (1) and (2) we conclude that for sufficiently large 
quasi-Monte
Carlo is superior to Monte Carlo.
However, in risk management 
is quite
modest, typically in the low thousands. On the other hand, the number of market
risk factors 
is large; often
is in the range
of a hundred to a thousand. For such values of 
and 
our test
results in the next section show that quasi-Monte Carlo remains superior to
Monte Carlo for the computation of VaR.
Test results
These results were obtained using the FINDER software system. FINDER may be obtained from Columbia University.
We used the generalized Faure low discrepancy sequence to calculate the Value at Risk, at a 98% confidence level, of two portfolios. We compared the results to those of Monte Carlo simulation. The low discrepancy method with a small sample yielded VaR estimates with 1% accuracy while the Monte Carlo, with the same sample size, had error about ten times larger.
For the first test we constructed a portfolio of 34 at-the-money equity and currency european call options. Each option is on a currency or equity index that is used as a single market risk factor. Therefore there are 34 market risk factors that influence the value of this portfolio and, therefore, the dimension of the problem is 34. We used J. P. Morgan/Reuters data sets for correlation and volatility of the corresponding market risk factors. We allocated $10,000 in each option for a total portfolio value of $340,000. We ran a Monte Carlo simulation which achieved sufficient accuracy using 100,000 points; we call this the true value. Figure 1 compares the low discrepancy method to Monte Carlo, each using a sample of 1,000 points. Two Monte Carlo simulations with different seeds are shown in the figure. The horizontal axis shows a probability interval around 98% and the vertical axis shows the corresponding VaR. The true value is shown for comparison. Figure 2 is similar to Figure 1. The only difference is that we have used antithetic variates in one of the Monte Carlo simulations. We see that antithetic variates do not yield any substantial improvement over simple Monte Carlo.
The second test was carried out using the Collateralized mortgage obligation (CMO) that one of the authors, S. Paskov, and J. F. Traub originally considered in 1993 when they first started applying low discrepancy sequences to problems in finance; see Paskov [1997] , Paskov and Traub [1995]. The CMO is from a pool of 30 year mortgages and has 10 tranches. In particular, we created a $1,000,000 portfolio by investing $100,000 in each of the tranches. Since we are dealing with 30 year mortgages with monthly payments the dimension of the problem is 360. As in the previous test, we ran a Monte Carlo simulation with 150,000 points to obtain the true VaR. Then we estimated the value at risk of the portfolio using Monte Carlo and the generalized Faure low discrepancy sequence, with 1,500 points each. Figure 3 shows the results. The horizontal axis depicts a probability interval around 98% and the vertical axis shows the corresponding VaR. Two Monte Carlo simulation results, with different seeds, and the result of the low discrepancy method are shown in the figure. The true value is also shown for comparison.
In summary, our tests indicate that small samples derived from low discrepancy sequences yield quite accurate VaR estimates. Monte Carlo with the same sample size has significantly larger error. Additional results may be found at http://www.cs.columbia.edu/~ap.
Concluding remarks
The efficiency of quasi-Monte Carlo methods for high dimensional integrals that arise in problems in finance has been discussed in a number of papers. These papers deal with the valuation of financial derivatives. In this paper we see that deterministic simulation using quasi-Monte Carlo methods provides a highly efficient alternative to Monte Carlo for VaR calculations.
The
error bound given in (1) shows that quasi-Monte Carlo is asymptotically
superior to Monte Carlo. Yet the test results indicate that quasi-Monte Carlo
retains its superior performance for modest 
an large 
often used in
risk management.
Here is a possible explanation. The error bound (1) is based on the Koksma-Hlawka inequality which holds for general integrands. Integrands in mathematical finance are usually non-isotropic. That is, some of the variables are more important than others. In a very recent paper Sloan and Wozniakowski [1998], Sloan and Wozniakowski formalize the notion of non-isotropic integrands and prove the existence of a quasi-Monte Carlo method with excellent convergence properties. Although their paper makes very significant progress, major open problems must still be solved before we fully understand why quasi-Monte Carlo is so superior to Monte Carlo for problems in mathematical finance.
This has been a first attempt in showing the effectiveness of quasi-Monte Carlo methods for risk management. We intend to continue this work by applying these methods to other market risk management problems. Credit risk management is another interesting application domain.
Acknowledgement
We wish to thank Joseph Traub for his valuable suggestions that greatly improved this paper.
References
Jorion., P., “Value at Risk,” McGraw-Hill, New York, 1997.
Niederreiter, H., “Random Number Generation and Quasi-Monte Carlo Methods,” SIAM, CBMS-NSF, 1992.
Ninomiya, S., and Tezuka, S., Toward real-time pricing of complex financial derivatives, Appl. Math. Finance, 3, 1996, 1-20.
Papageorgiou, A., and Traub, J. F., Beating Monte Carlo, Risk, 9:6, 1996, 63-65.
Paskov, S., New Methodologies for Valuing Derivatives, in “Mathematics for Derivative Securities,” M. Dempster and S. Pliska eds., Cambridge University Press, Cambridge, 1997, 545-582.
Paskov, S., and Traub, J. F., Faster Valuation of Financial Derivatives, Journal of Portfolio Management, Fall, 1995, 113-120.
Sloan, I., and Wozniakowski, H., When are Quasi-Monte Carlo Algorithms Efficient for High Dimensional Integrals?, J. Complexity, 4, 1998, 1-33.
Stuart, A., and Ord, J.K., “Kendall’s Advanced Theory of Statistics,” Volume 1, Distribution Theory, Halsted Press, New York,1994.
Tezuka, S., “Uniform Random Numbers: Theory and Practice,” Kluwer Academic Publishers, Boston, 1995.
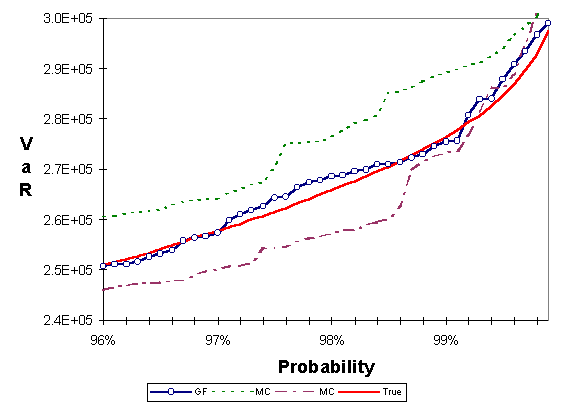
Figure 1: Portfolio of 34 equity and currency european call options. Comparison between Monte Carlo (MC) with two different seeds, and the generalized Faure (GF) low discrepancy method. Each method is using a sample of 1,000 points. True is the result of Monte Carlo using 100,000 points.
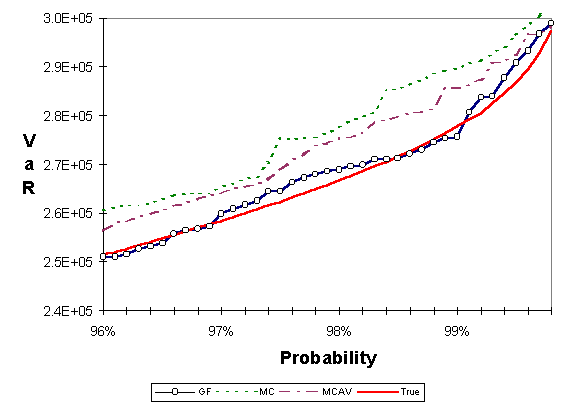
Figure 2: Portfolio of 34 equity and currency european call options. Comparison between Monte Carlo (MC), Monte Carlo with antithetic variates (MCAV), and the generalized Faure (GF) low discrepancy method. Each method is using a sample of 1,000 points. True is the result of Monte Carlo using 100,000 points.
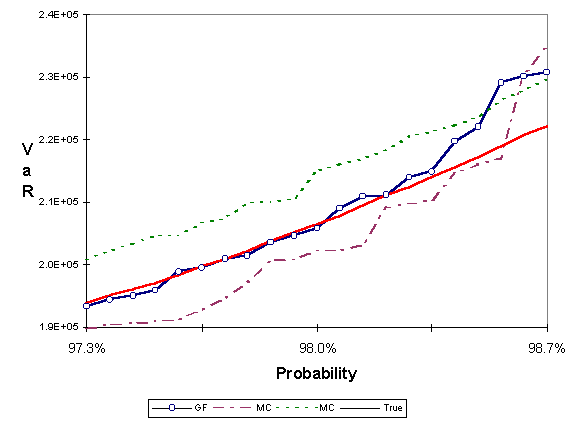
Figure 3: Portfolio of 10 CMO tranches. Comparison between Monte Carlo (MC) with two different seeds, and the generalized Faure (GF) low discrepancy method. Each method is using a sample of 1,500 points. True is the result of Monte Carlo using 150,000 points.